Advertisements
Advertisements
Question
In figure, arcs are drawn by taking vertices A, B and C of an equilateral triangle of side 10 cm. to intersect the sides BC, CA and AB at their respective mid-points D, E and F. Find the area of the shaded region (Use π = 3.14).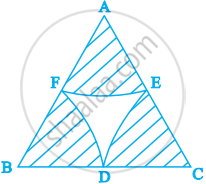
Solution
Since, ΔABC is an equilateral triangle.
∴ ∠A = ∠B = ∠C = 60°
And AB = BC = CA = 10 cm
E, F and D are mid-points of the given sides.
∴ AE = EC = CD = DB = BF = FA = 5 cm
Radius of a sector (r) = 5 cm
Now, area of sector CDE
= `θ/360^circ xx π"r"^2`
= `60^circ/360^circ xx 3.14 xx (5)^2 "cm"^2`
= `(3.14 xx 25)/6 "cm"^2`
= `78.5/6 "cm"^2`
= 13.0833 cm2
∴ Area of shaded region
= 3 (Area of sector CDE)
= 3 × 13.0833 cm2
= 39.25 cm2
APPEARS IN
RELATED QUESTIONS
A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. Find the areas of the corresponding minor and major segments of the circle. [Use π = 3.14 and `sqrt3 = 1.73`]
A sector of a circle of radius 8cm contains the angle of 135°. Find the area of sector.
The diagram shows a sector of circle of radius ‘r’ can containing an angle 𝜃. The area of sector is A cm2 and perimeter of sector is 50 cm. Prove that
(i) 𝜃 =`360/pi(25/r− 1)`
(ii) A = 25r – r2
A cow is tied with a rope of length 14 m at the corner of a rectangular field of dimensions 20 m × 16 m. Find the area of the field in which the cow can graze.
In the given figure, ABCD is a square of side 7 cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.

Four cows are tethered at the four corners of a square field of side 50 m such that each can graze the maximum unshared area. What area will be left ungrazed?
If angle of sector is 60°, radius is 3.5 cm then length of the arc is ____________.
The areas of two sectors of two different circles are equal. Is it necessary that their corresponding arc lengths are equal? Why?
Find the area of the minor segment of a circle of radius 14 cm, when the angle of the corresponding sector is 60°.
Find the area of the sector of a circle of radius 7 cm and of central angle 90°. Also, find the area of corresponding major sector.
