Advertisements
Advertisements
Question
A cow is tied with a rope of length 14 m at the corner of a rectangular field of dimensions 20 m × 16 m. Find the area of the field in which the cow can graze.
Solution
Let ABCD be a rectangular field.
Length of field = 20 m
Breadth of the field = 16 m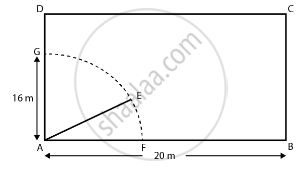
According to the question,
A cow is tied at a point A.
Let length of rope be AE = 14 m = l.
Angle subtended at the center of the sector = 90°
Angle subtended at the center (in radians) θ = `(90π)/180 = π/2`
∴ Area of a sector of a circle = `1/2 "r"^2θ`
= `1/2 xx (14)^2 xx (π/2)`
= 154 m2
Hence, the required area of a sector of a circle is 154 m2.
APPEARS IN
RELATED QUESTIONS
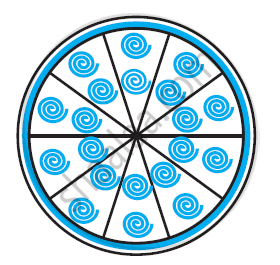
A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in figure. Find.
- The total length of the silver wire required.
- The area of each sector of the brooch [Use π = `22/7`]
To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships warned. [Use π = 3.14]
Area of a sector of angle p (in degrees) of a circle with radius R is ______.
Choose the correct alternative answer for the following question.
Find the perimeter of a sector of a circle if its measure is 90° and radius is 7 cm.
The radius of a circle with centre O is 7 cm. Two radii OA and OB are drawn at right angles to each other. Find the areas of minor and major segments.
If `theta` is the angle in degrees of a sector of a circle of radius V, then area of the sector is ____________.
A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 7 m long rope. The area of that part of the field in which the horse can graze is ____________.
In figure, a square is inscribed in a circle of diameter d and another square is circumscribing the circle. Is the area of the outer square four times the area of the inner square? Give reasons for your answer.
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
The length of the arc of a circle of radius 14 cm which subtends an angle of 60° at the centre of the circle is ______.
