Advertisements
Advertisements
Question
The radius of a circle with centre O is 7 cm. Two radii OA and OB are drawn at right angles to each other. Find the areas of minor and major segments.
Solution
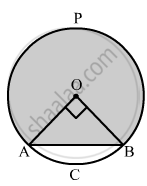
Area of minor segment = Area of sector AOBC − Area of right triangle AOB
`= (90°)/(360°) pi(OA)^2-1/2xx"OA"xx"OB"`
`=1/4xx22/7xx(7)^2-1/2xx7xx7`
`=1/4xx22/7xx(7)^2 - 1/2xx7xx7`
= 38.5 - 24.5
= 14 cm2
Area of major segment APB = Area of circle − Area of minor segment
`=(OA)^2 - 14`
`=22/7xx(7)^2-14`
= 154 - 14
= 140 cm2
Hence, the area of major segment is 140 cm2 .
APPEARS IN
RELATED QUESTIONS
Find the area of sector whose arc length and radius are 10 cm and 5 cm respectively
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes. [Use `pi = 22/7`]
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding:
Major sector [Use π = 3.14]
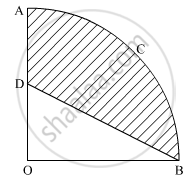
In the given figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the shaded region.
A sector of a circle of radius 8cm contains the angle of 135°. Find the area of sector.
A chord of a circle subtends an angle 𝜃 at the centre of circle. The area of the minor segment cut off by the chord is one eighth of the area of circle. Prove that 8 sin`theta/2 "cos"theta/2+pi =(pitheta)/45`
The radius of a circle is 10 cm. The area of a sector of the sector is 100 cm2. Find the area of its corresponding major sector. ( \[\pi\] = 3.14 ).
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the minor segment. [Use π = 3.14.]
A chord of length 6 cm is at a distance of 7.2 cm from the centre of a circle. Another chord of the same circle is of length 14.4 cm. Find its distance from the centre.
With vertices A, B and C of ΔABC as centres, arcs are drawn with radii 14 cm and the three portions of the triangle so obtained are removed. Find the total area removed from the triangle.
