Advertisements
Advertisements
Question
A chord of a circle subtends an angle 𝜃 at the centre of circle. The area of the minor segment cut off by the chord is one eighth of the area of circle. Prove that 8 sin`theta/2 "cos"theta/2+pi =(pitheta)/45`
Solution
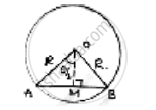
Let radius of circle = r
Area of circle = 𝜋𝑟2
AB is a chord, OA, OB are joined drop OM ⊥ AB. This OM bisects AB as well as ∠AOB.
∠AOM = ∠MOB =`1/2(0) =theta/2` AB = 2AM
In ΔAOM, ∠AMO = 90°
`"Sin"theta/2=(AM)/(AD)⇒ AM = R."sin"theta/2` AB = 2R sin`theta/2`
`"Cos"theta/2=(OM)/(AD)⇒ OM = R"cos"theta/2`
Area of segment cut off by AB = (area of sector) – (area of triangles)
=`theta/360× pir^2 −1/2`× 𝐴𝐵 × 𝑂𝑀
`= r^2 [(pitheta)/360^@−1/2. 2"rsin"theta/2. R" cos"theta/2]`
`= R^2 [(pitheta)/360^@− "sin"theta/2. "cos"theta/2]`
Area of segment =`1/2`(𝑎𝑟𝑒𝑎 𝑜𝑓 𝑐𝑖𝑟𝑐𝑙𝑒)
`r^2 [(pitheta)/360− "sin"theta/2." cos"theta/2] =1/8pir^2`
`(8pitheta)/360^@− 8 "sin"theta/2. "cos"theta/2= pi`
`8 "sin"theta/2. "cos"theta/2+ pi =(pitheta)/45`
APPEARS IN
RELATED QUESTIONS
In Fig. 3, AP and BP are tangents to a circle with centre O, such that AP = 5 cm and ∠APB = 60°. Find the length of chord AB.
The perimeter of certain sector of circle of radius 5.6 m is 27.2 m. Find the area of sector.
A chord of circle of radius 14cm makes a right angle at the centre. Find the areas of minor and major segments of the circle.

In the given figure, if A is the centre of the circle. \[\angle\] PAR = 30°, AP = 7.5, find the area of the segment PQR. (\[\pi\] = 3.14)

In a circle of radius 7 cm, a square ABCD is inscribed. Find the area of the circle which is outside the square.
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
In figure, arcs have been drawn of radius 21 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
With vertices A, B and C of ΔABC as centres, arcs are drawn with radii 14 cm and the three portions of the triangle so obtained are removed. Find the total area removed from the triangle.
The area of the sector of a circle of radius 12 cm is 60π cm2. The central angle of this sector is ______.
