Question

AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`

Answer 1

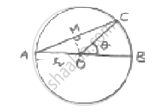
Given AB is diameter of circle with centre O

∠COB = 𝜃

Area of sector BOC =`theta/360^@× pir^2`

Area of segment cut off, by AC = (area of sector) – (area of ΔAOC)

∠AOC = 180 – 𝜃 [∠AOC and ∠BOC form linear pair]

Area of sector =`(180−theta)/360^@× pir^2 = (pir^2)/2−(pithetar)^2/360^@`

In ΔAOC, drop a perpendicular AM, this bisects ∠AOC and side AC.

Now, In ΔAMO, sin∠AOM =`(AM)/(DA)⇒ sin ((180−theta)/2) =(AM)/R`

⇒ AM = R sin(90 −`theta/2`) = 𝑅. cos`theta/2`

cos ∠ADM =`(OM)/(OA)⇒ cos (90 −theta/2) =(OM)/Y⇒ OM = R. "sin"theta/2`

Area of segment =`(pir^2)/2−(pithetar^2)/360^@−1/2`(𝐴𝐶 × 𝑂𝑀) [𝐴𝐶 = 2 𝐴𝑀]

`=(pir^2)/2−(pithetar^2)/360^@−1/2× (2 R "cos"theta/2R "sin"theta/2)`

`= r^2 [pi/2−(pitheta)/360^@−"cos"theta/2"sin"theta/2]`

Area of segment by AC = 2 (Area of sector BDC)`

`r^2[pi/2−(pitheta)/360^@− "cos"theta/2." sin"theta/2] = 2r^2 [(pitheta)/360^@]`

`"cos"theta/2." sin"theta/2=pi/2−(pitheta)/360−(2pitheta)/360^@`

`=pi/2−(pitheta)/360^@[1 + 2]`

`=pi/2−(pitheta)/360^@= pi(1/2−theta/120^@)`

`"cos"theta/2. "sin"theta/2= pi (1/2−theta/120^@)`