Advertisements
Advertisements
Question
In the following figure, if m(are DXE) = 90° and m(are AYC) = 30°. Find ∠DBE.

Solution

By inscribed angle theorem,
m∠AEB=(1/2) × m∠AYC=(1/2) × 30o = 15o ...(1)
m∠EAD=(1/2) × m∠DXE=(1/2) × 90o = 45o ...(2)
∠DBE + ∠AEB = ∠EAD
⇒ m∠DBE + 15o = 45o
⇒ m∠DBE = 45o - 15o = 30o
APPEARS IN
RELATED QUESTIONS
Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60° [Use `pi = 22/7`]
Find the area of a quadrant of a circle whose circumference is 22 cm. [Use `pi = 22/7`]
AB is a chord of circle with centre O and radius 4cm. AB is length of 4cm. Find the area of sector of the circle formed by chord AB
The perimeter of certain sector of circle of radius 5.6 m is 27.2 m. Find the area of sector.
A sector of 56° cut out from a circle contains area of 4.4 cm2. Find the radius of the circle
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`
A chord of a circle subtends an angle 𝜃 at the centre of circle. The area of the minor segment cut off by the chord is one eighth of the area of circle. Prove that 8 sin`theta/2 "cos"theta/2+pi =(pitheta)/45`

The radius of a circle is 17.5 cm. Find the area of the sector enclosed by two radii and an arc 44 cm in length.
Four cows are tethered at the four corners of a square field of side 50 m such that the each can graze the maximum unshared area. What area will be left ungrazed?
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
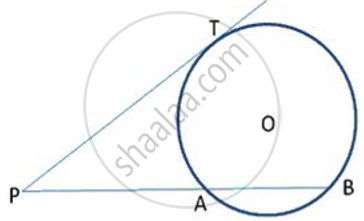
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
The diameter of a sphere is 6 cm, Find the total surface area of the sphere. (π = 3.14)
In figure, arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region.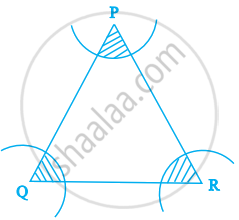
Three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these circles.
Find the difference of the areas of two segments of a circle formed by a chord of length 5 cm subtending an angle of 90° at the centre.
The length of the minute hand of a clock is 6 cm. Find the area swept by it when it moves from 7:05 p.m. to 7:40 p.m.
Find the area of the sector of a circle of radius 7 cm and of central angle 90°. Also, find the area of corresponding major sector.
