Advertisements
Advertisements
Question
In figure, arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region.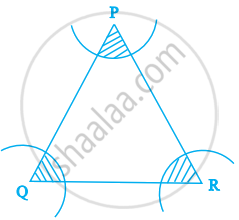
Solution
Given that, radii of each arc (r) = 14 cm
Now, area of the sector with central angle P
=
=
Area of the sector with central angle Q
=
=
And area of the sector with central angle R
=
=
Therefore, sum of the areas of three sectors
=
=
=
= 98π
=
= 14 × 22
= 308
Hence, the required area of the shaded region is 308 cm2.
APPEARS IN
RELATED QUESTIONS
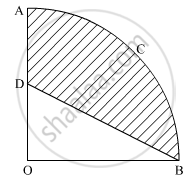
In the given figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the shaded region.
In a circle of radius 35 cm, an arc subtends an angle of 72° at the centre. Find the length of arc and area of sector
The diameter of a sphere is 6 cm, Find the total surface area of the sphere. (π = 3.14)
The area of the shaded portion in the following figure is equal to the area of.
In figure, arcs are drawn by taking vertices A, B and C of an equilateral triangle of side 10 cm. to intersect the sides BC, CA and AB at their respective mid-points D, E and F. Find the area of the shaded region (Use π = 3.14).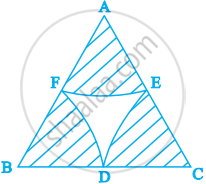
Sides of a triangular field are 15 m, 16 m and 17 m. With the three corners of the field a cow, a buffalo and a horse are tied separately with ropes of length 7 m each to graze in the field. Find the area of the field which cannot be grazed by the three animals.
In figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and distance between AB and DC = 14 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region of the figure.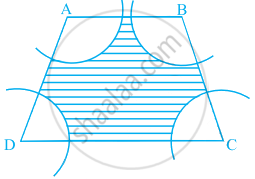
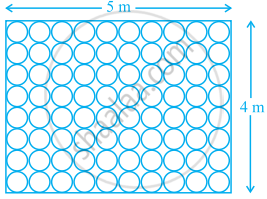
Floor of a room is of dimensions 5 m × 4 m and it is covered with circular tiles of diameters 50 cm each as shown in figure. Find the area of floor that remains uncovered with tiles. (Use π = 3.14)
The length of the arc of a circle of radius 14 cm which subtends an angle of 60° at the centre of the circle is ______.
With vertices A, B and C of ΔABC as centres, arcs are drawn with radii 14 cm and the three portions of the triangle so obtained are removed. Find the total area removed from the triangle.
