Advertisements
Advertisements
Question
A circular park is surrounded by a road 21 m wide. If the radius of the park is 105 m, find the area of the road.
Solution
Circular road and park are concentric circles.
Radius of the park = r1 = 105 m
Width of road = 21 m
Radius of circular road and park = r2
= 105 m + 21 m
= 126 m
So, Area of road = Area of park and road – Area of park
= `π"r"_2^2 - π"r"_1^2`
= `π["r"_2^2 - "r"_1^2]`
= `22/7 [(126)^2 - (105)^2]`
= `22/7 [126 - 105][126 + 105]`
= `22/7 xx 21 xx 231`
= 22 × 3 × 231
= 66 × 231
= 15246 cm2
∴ Area of road = 15246 cm2
APPEARS IN
RELATED QUESTIONS
Find the cost of polishing a circular table-top of diameter 1.6 m, if the rate of polishing is ₹ 15/m2. (Take π = 3.14)
A room 4.9 m long and 3.5 m board is covered with carpet, leaving an uncovered margin of 25 cm all around the room. If the breadth of the carpet is 80 cm, find its cost at ₹ 80 per metre.
Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD = 9 cm, CD = 12 cm, ∠ACB=90° and AC = 15 cm.

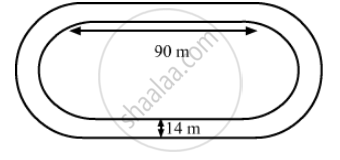
The inside perimeter of a running track (shown in the following figure) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If the track is everywhere 14 m wide. find the area of the track. Also find the length of the outer running track.
If the circumference and the area of a circle are numerically equal, then diameter of the circle is
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then its radius is
ABCD is a field in the shape of a trapezium, AD || BC, ∠ABC = 90° and ∠ADC = 60°. Four sectors are formed with centres A, B, C and D, as shown in the figure. The radius of each sector is 14 m. Find the following:
- total area of the four sectors,
- area of the remaining portion, given that AD = 55 m, BC = 45 m and AB = 30 m.

The wheel of a cart is making 5 revolutions per second. If the diameter of the wheel is 84 cm, find its speed in km per hour.
In the given figure, an equilateral triangle has been inscribed in a circle of radius 4 cm. Find the area of the shaded region.

The ratio of the area of a circle to the area of its semicircle is
