Advertisements
Advertisements
Question
In the given figure, an equilateral triangle has been inscribed in a circle of radius 4 cm. Find the area of the shaded region.

Solution
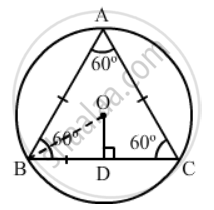
Draw
OD ⊥ BC
.
Because ΔABC is equilateral, ∠A = ∠B = ∠C = 60° .
Thus, we have:
∠OBD = 30°
`⇒ "OD"/"OB" = sin 30°`
`=> "OD"/"OB" = 1/2`
`=>"OB" = (1/2)`
`=> "OD" = (1/2xx4)"cm" [therefore "OB" = "radius"]`
⇒ OD =2 cm
⇒ BD2 = (OB2 - OD2) [By Pythagoras 'Therom']
⇒ BD2 = (42 - 22) cm2
⇒ BD2 = (16 - 4) cm2
⇒ BD2 = 12 cm2
`⇒ "BD" = 2sqrt(3)`
Also
BC = 2 × BD
`=>(2xx2sqrt(3))`
`=4sqrt(3)`
∴ Area of the shaded region = (Area of the circle) - (Area of Δ)
`=|(3.14xx4xx4)-(sqrt(3)/4xx4sqrt(3)xx4sqrt(3))|"cm"^2`
`= |50.24 - (12xx1.73)| "cm"^2`
= (50.24 - 20.76) cm2
= 29.48 cm2
APPEARS IN
RELATED QUESTIONS
The cost of harvesting a square field at ₹ 900 per hectare is ₹ 8100. Find the cost of putting a fence around it at ₹ 18 per meter.
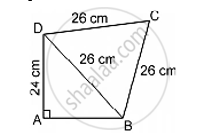
Find the area of the quadrilateral ABCD in which AD = 24 cm, ∠BAD 90° and ∠BCD is an equilateral triangle having each side equal to 26 cm. Also, find the perimeter of the quadrilateral.
A circle is inscribed in an equilateral triangle ABC is side 12 cm, touching its sides (the following figure). Find the radius of the inscribed circle and the area of the shaded part.

If the circumference of two circles are in the ratio 2 : 3, what is the ratio of their areas?
Write the formula for the area of a sector of angle \[\theta\] (in degrees) of a circle of radius r.
The area of the circle that can be inscribed in a square of side 10 cm is
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex of an equilateral triangle of side 12 cm as centre and a sector of circle of radius 6 cm with centre B is made.
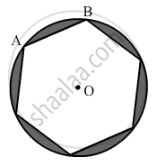
A round table cover has six equal designs as shown in the given figure. If the radius of the cover is 35 cm, then find the total area of the design.
Thenmozhi wants to level her circular flower garden whose diameter is 49 m at the rate of ₹ 150 per m2 Find the cost of levelling
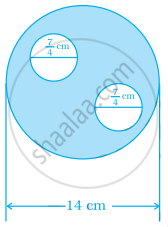
Find the area of the shaded region: