Advertisements
Advertisements
Question
Thenmozhi wants to level her circular flower garden whose diameter is 49 m at the rate of ₹ 150 per m2 Find the cost of levelling
Solution
Diamter of the circular garden d = 49 m
Radius r = `"d"/2 = 49/2` m
Area of the circular garden = πr2 sq.units
= `22/7 xx 49/2 xx 49/2 "m"^2`
= 1,886.5 m2
Cost of levelling a m2 area = ₹ 150
∴ Cost of levelling 1886.5 m2 = ₹ 150 × 1886.5
= ₹ 2,82,975
Cost of levelling the flower garden = ₹ 2,82,975
APPEARS IN
RELATED QUESTIONS
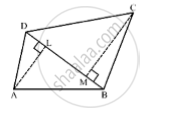
In the given figure ABCD is quadrilateral in which diagonal BD = 24 cm, AL ⊥ BD and CM ⊥ BD such that AL = 9cm and CM = 12 cm. Calculate the area of the quadrilateral.
Find the area enclosed between two concentric circles of radii 3.5 cm and 7 cm. A third concentric circle is drawn outside the 7 cm circle , such that the area enclosed between it and the 7 cm circle is same as that between the two inner circles . Find the radius of the third circle correct to one decimal place.
The area of sector is one-twelfth that of the complete circle. Find the angle of the sector .
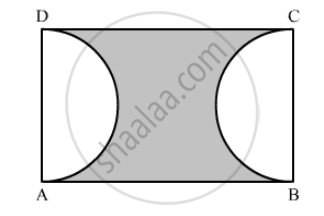
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the length of the boundary of the shaded region.
In a circle of radius 10 cm, an arc subtends an angle of 108° at the centre. what is the area of the sector in terms of π?
The radius of a wheel is 0.25 m. The number of revolutions it will make to travel a distance of 11 km will be
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then its radius is
ABCD is a rectangle whose three vertices are B (4,0), C (4,3) and D (0, 3). The length of one of its diagonals is
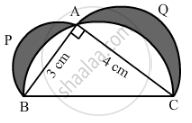
In the given figure, ∆ABC is right-angled at A. Semicircles are drawn on AB, AC and BC as diameters. It is given that AB = 3 cm and AC = 4 cm. Find the area of the shaded region.
The diameter of a wheel is 40 cm. How many revolutions will it make in covering 176 m?
