Advertisements
Advertisements
Question
In a circle of radius 10 cm, an arc subtends an angle of 108° at the centre. what is the area of the sector in terms of π?
Solution
We have given the radius of the circle and angle subtended at the centre of the circle.
`r=10 cm`
`θ=108°`
Now we will find the area of the sector.
Area of the sector=`θ/360 xxpir^2`
Substituting the values we get,
Area of the sector=` 108/360xxpixx10^2` ...........(1)
Now we will simplify the equation (1) as below,
Area of the sector =`3/10xxpixx100`
Area of the sector =`3xxpixx10`
⇒ Area of the sector =`30 pi`
Therefore, area of the sector is`30 picm^2`
APPEARS IN
RELATED QUESTIONS
Find the length of the hypotenuse of an isosceles right-angled triangle whose area is `200^2` cm . Also, find its perimeter
In Figure 5, a circle is inscribed in a triangle PQR with PQ = 10 cm, QR = 8 cm and PR =12 cm. Find the lengths of QM, RN and PL ?

In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the sector formed by the arc. (Use π = `22/7`)
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
Write the formula for the area of a segment in a circle of radius r given that the sector angle is \[\theta\] (in degrees).
If diameter of a circle is increased by 40%, then its area increase by
If a chord of a circle of radius 28 cm makes an angle of 90 ° at the centre, then the area of the major segment is
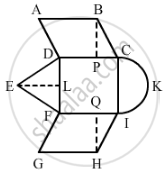
A child draws the figure of an aeroplane as shown. Here, the wings ABCD and FGHI are parallelograms, the tail DEF is an isosceles triangle, the cockpit CKI is a semicircle and CDFI is a square. In the given figure, BP ⊥ CD, HQ ⊥ FI and EL ⊥ DF. If CD = 8 cm, BP = HQ = 4 cm and DE = EF = 5 cm, find the area of the whole figure.
Two circles touch each other externally. The sum of their areas is 58π cm2 and the distance between their centers is 10 cm. Find the radii of the two circles.
Find the diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm.
