Advertisements
Advertisements
प्रश्न
In a circle of radius 10 cm, an arc subtends an angle of 108° at the centre. what is the area of the sector in terms of π?
उत्तर
We have given the radius of the circle and angle subtended at the centre of the circle.
`r=10 cm`
`θ=108°`
Now we will find the area of the sector.
Area of the sector=`θ/360 xxpir^2`
Substituting the values we get,
Area of the sector=` 108/360xxpixx10^2` ...........(1)
Now we will simplify the equation (1) as below,
Area of the sector =`3/10xxpixx100`
Area of the sector =`3xxpixx10`
⇒ Area of the sector =`30 pi`
Therefore, area of the sector is`30 picm^2`
APPEARS IN
संबंधित प्रश्न
A calf is tied with a rope of length 6 m at the corner of a square grassy lawn of side 20 m . If the length of the rope is increased by 5.5 m , find the increase in area of the grassy lawn in which the calf can graze .
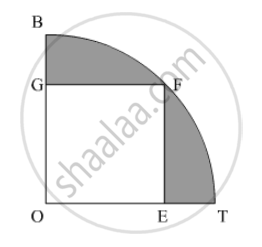
In the following figure, OE = 20 cm. In sector OSFT, square OEFG is inscribed. Find the area of the shaded region.
In the following figure, the boundary of the shaded region consists of four semi-circular arcs, the smallest two being equal. If the diameter of the largest is 14 cm and of the smallest is 3.5 cm, find
the length of the boundary.
the area of the shaded region.

In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the perimeter of the cross-section
In the following figure, ABC is an equilateral triangle of side 8 cm. A, B and C are the centres of circular arcs of radius 4 cm. Find the area of the shaded region correct upto 2 decimal places. (Take π =3.142 and`sqrt3` = 1.732).

In the given figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region. [Use π= 3.14]

The diameter of the wheels of a bus is 140 cm. How many revolutions per minute do the wheels make when the bus is moving at a speed of 72.6 km per hour?
Find the area of a ring-shaped region enclosed between two concentric circles of radii 20 cm and 15 cm.
A circular field of radius 105 m has a circular path of uniform width of 5 m along and inside its boundary. Find the area of the path.
Is the area of the largest circle that can be drawn inside a rectangle of length a cm and breadth b cm (a > b) is πb2 cm2? Why?
