Advertisements
Advertisements
Question
Write the formula for the area of a sector of angle \[\theta\] (in degrees) of a circle of radius r.
Solution
Let r be the radius of the circle and angle θ subtended at the centre of the circle.
Area of the sector of the circle =`θ/360xxpir^2`
Therefore, area of the sector is =`θ/360xxpir^2`
APPEARS IN
RELATED QUESTIONS
If the circumference of two circles are in the ratio 2 : 3, what is the ratio of their areas?
If a square is inscribed in a circle, what is the ratio of the areas of the circle and the square?
The area of a circular path of uniform width h surrounding a circular region of radius r is
ABCD is a rectangle whose three vertices are B (4,0), C (4,3) and D (0, 3). The length of one of its diagonals is
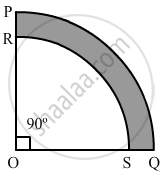
In the given figure, PQRS represents a flower bed. If OP = 21 m and OR = 14 m, find the area of the flower bed.
A racetrack is in the form of a ring whose inner circumference is 352 m and outer circumference is 396 m. Find the width and the area of the track.
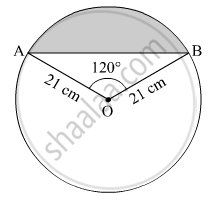
Find the area of the segment shown in Fig. 2, if the radius of the circle is 21 cm and ∠AOB = 120° `( "Use" π = (22)/(7))`
Find the area of a circle of radius 30 cm (use π = 3.14).
Perimeter of a sector of a circle whose central angle is 90° and radius 7 cm is ____________.
Area of a circle with diameter ‘m’ radius ‘n’ and circumference ‘p’ is ______.
