Advertisements
Advertisements
प्रश्न
Write the formula for the area of a sector of angle \[\theta\] (in degrees) of a circle of radius r.
उत्तर
Let r be the radius of the circle and angle θ subtended at the centre of the circle.
Area of the sector of the circle =`θ/360xxpir^2`
Therefore, area of the sector is =`θ/360xxpir^2`
APPEARS IN
संबंधित प्रश्न
Find the length of the hypotenuse of an isosceles right-angled triangle whose area is `200^2` cm . Also, find its perimeter
In Figure 5, a circle is inscribed in a triangle PQR with PQ = 10 cm, QR = 8 cm and PR =12 cm. Find the lengths of QM, RN and PL ?

Find the area enclosed between two concentric circles of radii 3.5 cm and 7 cm. A third concentric circle is drawn outside the 7 cm circle , such that the area enclosed between it and the 7 cm circle is same as that between the two inner circles . Find the radius of the third circle correct to one decimal place.
A rectangular park is 100 m by 50 m. It is surrounding by semi-circular flower beds all round. Find the cost of levelling the semi-circular flower beds at 60 paise per square metre (use π = 3.14).
Find the ratio of the area of the circle circumscribing a square to the area of the circle inscribed in the square .
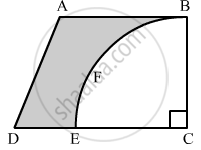
From a thin metallic piece in the shape of a trapezium ABCD in which AB || CD and ∠BCD = 90°, a quarter circle BFEC is removed. Given, AB = BC = 3.5 cm and DE = 2 cm, calculate the area of remaining (shaded) part of metal sheet.
The diameter of the wheels of a bus is 140 cm. How many revolutions per minute do the wheels make when the bus is moving at a speed of 72.6 km per hour?
Find the area of the shaded portion in each of the following diagrams:
(i)

(ii)

The following figure shows two circles with the same center. The radius of the larger circle is 10 cm and the radius of the smaller circle is 4 cm.

Find:
(a) the area of the larger circle
(b) the area of the smaller circle
(c) the shaded area between the two circles. (π = 3.14)
Is the area of the circle inscribed in a square of side a cm, πa2 cm2? Give reasons for your answer.
