Advertisements
Advertisements
प्रश्न
Find the ratio of the area of the circle circumscribing a square to the area of the circle inscribed in the square .
उत्तर
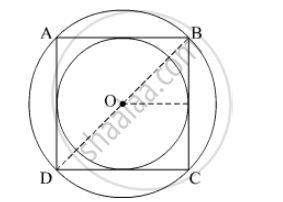
Let the side of the square inscribed in a square be a units.
Diameter of the circle outside the square = Diagonal of the square = \[\sqrt{2}a\]
Radius = \[\frac{\sqrt{2}a}{2} = \frac{a}{\sqrt{2}}\]
So, the area of the circle circumscribing the square =\[\pi \left( \frac{a}{\sqrt{2}} \right)^2\] .....(i)
Now, the radius of the circle inscribed in a square =\[\frac{a}{2}\]
Hence, area of the circle inscribed in a square = \[\pi \left( \frac{a}{2} \right)^2\] .....(ii)
From (i) and (ii)
\[ = \frac{\frac{1}{2}}{\frac{1}{4}}\]
\[ = \frac{2}{1}\]
Hence, the required ratio is 2 : 1.
APPEARS IN
संबंधित प्रश्न
The area of a parallelogram is `392m^2` . If its altitude is twice the corresponding base, determined the base and the altitude.
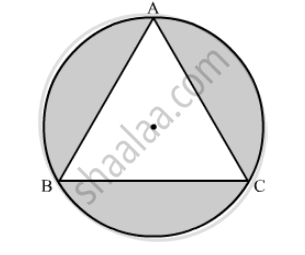
In the following figure, an equilateral triangle ABC of side 6 cm has been inscribed in a circle. Find the area of the shaded region. (Take π = 3.14).
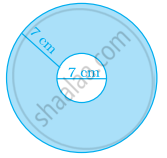
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
The radius of a circle is 20 cm. It is divided into four parts of equal area by drawing three concentric circles inside it. Then, the radius of the largest of three concentric circles drawn is
ABCD is a square of side 4 cm. If E is a point in the interior of the square such that ΔCEDis equilateral, then area of Δ ACE is
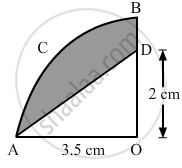
In the given figure, OABC is a quadrant of a circle of radius 3.5 cm with centre O. If OD = 2 cm, find the area of the shaded portion.
The diameter of the wheels of a bus is 140 cm. How many revolutions per minute do the wheels make when the bus is moving at a speed of 72.6 km per hour?
The diameters of three wheels are in the ratio 2 : 4 : 8. If the sum of the circumferences of these circles be 132 cm, find the difference between the areas of the largest and the smallest of these wheels.
Find the area of the shaded region:
A table cover of dimensions 3 m 25 cm × 2 m 30 cm is spread on a table. If 30 cm of the table cover is hanging all around the table, find the area of the table cover which is hanging outside the top of the table. Also find the cost of polishing the table top at ₹ 16 per square metre.
