Advertisements
Advertisements
प्रश्न
The diameters of three wheels are in the ratio 2 : 4 : 8. If the sum of the circumferences of these circles be 132 cm, find the difference between the areas of the largest and the smallest of these wheels.
उत्तर
Let the diameters of three wheel be
d1 = 2x ⇒ r1 = x
d2 = 4x ⇒ r2 = 2x
d3 = 8x ⇒ r3 = 4x
Now,
2πr1 + 2πr2 + 2πr3 = 132
⇒ 2π(r1 + r2 + r3) = 132
⇒ x + 2x + 4x = `66 xx (7)/(22)`
⇒ 7x = 21
⇒ x = 3cm
∴ DIfference between the areas of the largest and the smallest wheels
= πr32 - πr12
= π(4 x 3)2 - π(3)2
= 144π - 9π
= 135π
= `135 xx (22)/(7)`
= 424.29cm2.
APPEARS IN
संबंधित प्रश्न
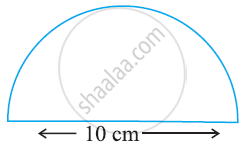
Find the perimeter of the adjoining figure, which is a semicircle including its diameter.
A room 4.9 m long and 3.5 m board is covered with carpet, leaving an uncovered margin of 25 cm all around the room. If the breadth of the carpet is 80 cm, find its cost at ₹ 80 per metre.
A carpet is laid on floor of a room 8 m by 5 m. There is border of constant width all around the carpet. If the area of the border is `12m^2` find its width.
Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD = 9 cm, CD = 12 cm, ∠ACB=90° and AC = 15 cm.

Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
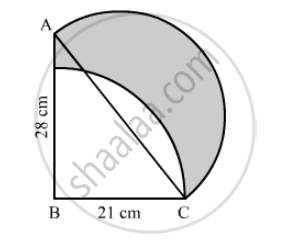
In the following figure, ABC is a right-angled triangle, ∠B = 90°, AB = 28 cm and BC = 21 cm. With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
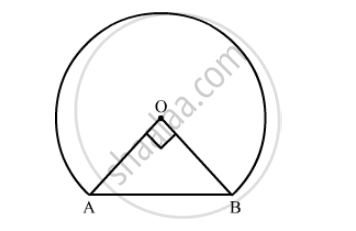
In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the area of the cross-section.
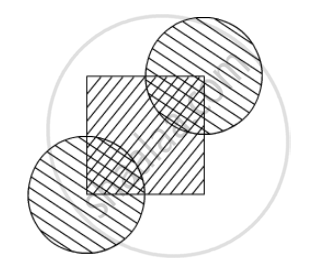
In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O' are centres of the circles. Find the area of shaded region.
If AB is a chord of length \[5\sqrt{3}\] cm of a circle with centre O and radius 5 cm, then area of sector OAB is
The area of a sector whose perimeter is four times its radius r units, is
