Advertisements
Advertisements
प्रश्न
If AB is a chord of length \[5\sqrt{3}\] cm of a circle with centre O and radius 5 cm, then area of sector OAB is
पर्याय
\[\frac{3\pi}{8}c m^2 \]
\[\frac{8\pi}{3}c m^2\]
\[25 \pi cm^2\]
\[\frac{25\pi}{3}c m^2\]
उत्तर
We have to find the area of the sector OAB.

We have,
`AM=(5sqrt3)/2`
So,
sin` ∠ AOM=(5sqrt3)/(2(5))`
Hence,
`∠ AOM=60°`
Therefore area of the sector,
`=1/2r^2θ`
`=1/2 (25)(2pi/3)`
`=(25pi)/3 cm^2`
APPEARS IN
संबंधित प्रश्न
Prove that the area of a circular path of uniform width h surrounding a circular region of radius r is `pih(2r+h)`
In the following figure, ABCD is a rectangle with AB = 14 cm and BC = 7 cm. Taking DC, BC and AD as diameters, three semi-circles are drawn as shown in the figure. Find the area of the shaded region.
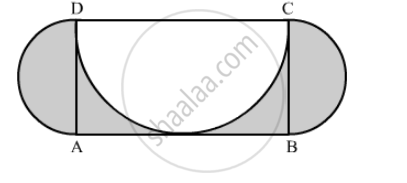
The area of the largest triangle that can be inscribed in a semi-circle of radius r, is
The area of a circle is 220 cm2. The area of ta square inscribed in it is
Find the area of the major segment APB of a circle of radius 35 cm and ∠AOB = 90°, as shown in the given figure.
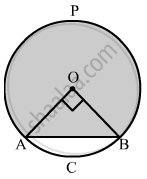
If the sum of the areas of two circles with radii R1 and R2 is equal to the area of a circle of radius R, then ______.
Two circles touch each other externally. The sum of their areas is 58π cm2 and the distance between their centers is 10 cm. Find the radii of the two circles.
A bicycle wheel, diameter 56 cm, is making 45 revolutions in every 10 seconds. At what speed in kilometre per hour is the bicycle traveling?
A roller has a diameter of 1.4 m. Find :
(i) its circumference ;
(ii) the number of revolutions it makes while travelling 61.6 m.
Read the following passage:
People of a circular village Dharamkot want to construct a road nearest to it. The road cannot pass through the village. But the people want the road at a shortest distance from the centre of the village. Suppose the road starts from A which is outside the circular village (as shown in the figure) and touch the boundary of the circular village at B such that AB = 20 m. Also the distance of the point A from the centre O of the village is 25 m. |
Based on the above information, answer the following questions:
- If B is the mid-point of AC, then find the distance AC.
- Find the shortest distance of the road from the centre of the village.
- Find the circumference of the village.
OR
Find the area of the village.


