Advertisements
Advertisements
प्रश्न
Read the following passage:
People of a circular village Dharamkot want to construct a road nearest to it. The road cannot pass through the village. But the people want the road at a shortest distance from the centre of the village. Suppose the road starts from A which is outside the circular village (as shown in the figure) and touch the boundary of the circular village at B such that AB = 20 m. Also the distance of the point A from the centre O of the village is 25 m. |
Based on the above information, answer the following questions:
- If B is the mid-point of AC, then find the distance AC.
- Find the shortest distance of the road from the centre of the village.
- Find the circumference of the village.
OR
Find the area of the village.
उत्तर

i. B is the mid-point of AC
∴ AC = 2AB
AC = 2 × 20 = 40 m
ii. Shortest distance of the road from the centre of circle = Radius of circle
In ΔOAB, ∠B = 90°
∴ OB2 + AB2 = OA2
OB2 + 202 = 252
OB2 = 625 – 400
OB = `sqrt(225)` = 15
∴ Shortest distance = 15 m
iii. Circumference of the village
= 2πr
= `2 xx 22/7 xx 15`
= `660/7`
= `94 2/7 "m"`
OR
iii. Area of the village
= πr2
= `22/7 xx 15 xx 15`
= `4950/7`
= `707 1/7 "m"^2`
APPEARS IN
संबंधित प्रश्न
One side of a rectangle is 12 cm long and its diagonal measure 37 cm. Find the other side and the area of the rectangle.
A calf is tied with a rope of length 6 m at the corner of a square grassy lawn of side 20 m . If the length of the rope is increased by 5.5 m , find the increase in area of the grassy lawn in which the calf can graze .
In the following figure, there are three semicircles, A, B and C having diameter 3 cm each, and another semicircle E having a circle D with diameter 4.5 cm are shown. Calculate:
(i) the area of the shaded region
(ii) the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.

The ratio of the outer and inner perimeters of a circular path is 23 : 22. If the path is 5 metres wide, the diameter of the inner circle is
The areas of two concentric circles are 1386 cm2 and 962.5 cm2. The width of the ring is
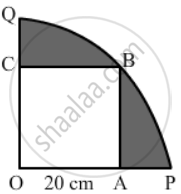
In the given figure, a square OABC has been inscribed in the quadrant OPBQ. If OA = 20 cm, then the area of the shaded region is
The sum of diameters of two circles is 112cm and the sum of their areas is 5236cm2. Find the radii of the two circles.
Area of circle of radius ‘n’ units is
Is the area of the circle inscribed in a square of side a cm, πa2 cm2? Give reasons for your answer.
Area of the circle obtained in 196 m2 is ______.


