Advertisements
Advertisements
प्रश्न
In the given figure, a square OABC has been inscribed in the quadrant OPBQ. If OA = 20 cm, then the area of the shaded region is
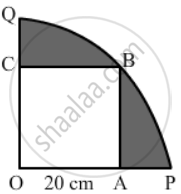
पर्याय
214 cm2
228 cm2
242 cm2
248 cm2
उत्तर
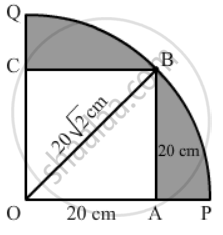
228 cm2
Join OB.
Now, OB is the radius of the circle.
We have :
OB2 = OA + AB [By pythagoras' therom]
⇒ OB2 = {(20)2 + (20)2} cm2
⇒ OB2 =(400+400) cm2
⇒ OB2 = 800 cm2
`=> "OB" =20sqrt2 "cm"`
Hence, the radius of the circle is `20sqrt(2) "cm".`
Now,
Area of the shaded region = Area of the quadrant - Area of the square OABC\
`=|(1/4xx3.14xx20sqrt(2)xx20sqrt(2))-(20xx20)| "cm"^2`
`=|(1/4xx314/100xx800)-400| "cm"^2`
=(628-400) cm2
= 228 cm2
APPEARS IN
संबंधित प्रश्न
Find the cost of polishing a circular table-top of diameter 1.6 m, if the rate of polishing is ₹ 15/m2. (Take π = 3.14)
The length and breadth of a rectangular garden are in the ratio 9:5. A path 3.5 m wide, running all around inside it has an area of `1911m^2` . Find the dimensions of the garden.
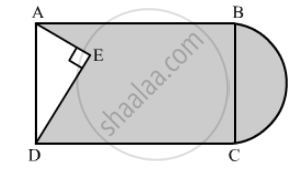
In the following figure, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside' the region. Find the area of the shaded region. [Use π =]`22/7` [CBSE 2014]
A child makes a poster on a chart paper drawing a square ABCD of side 14 cm. She draws four circles with centre A, B, C and D in which she suggests different ways to save energy. The circles are drawn in such a way that each circle touches externally two of the three remaining circles (in the following figure). In the shaded region she write a message 'Save Energy'. Find the perimeter and area of the shaded region.
(Use π = 22/7)

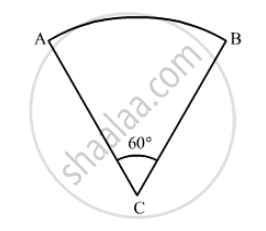
If the adjoining figure is a sector of a circle of radius 10.5 cm, what is the perimeter of the sector? (Take \[\pi = 22/7\])
If the diameter of a semi-circular protractor is 14 cm, then find its perimeter.
If the difference between the circumference and radius of a circle is 37 cm, then its area is
A wire is bent to form a square enclosing an area of 484 cm2. Using the same wire, a circle is formed. Find the area of the circle.
The length of an arc of a circle, subtending an angle of 54° at the centre, is 16.5 cm. Calculate the radius, circumference and area of the circle.
A horse is tethered to one corner of a field which is in the shape of an equilateral triangle of side 12 m. If the length of the rope is 7 m, find the area of the field which the horse cannot graze. Write the answer correct to 2 places of decimal.
