Advertisements
Advertisements
प्रश्न
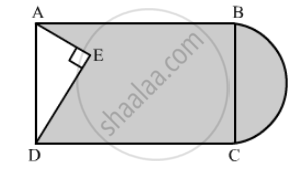
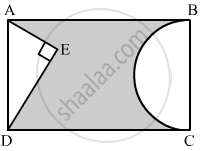
In the following figure, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside' the region. Find the area of the shaded region. [Use π =]`22/7` [CBSE 2014]
उत्तर
In right triangle AED
AD2 = AE2 + DE2
= (9)2 + (12)2
= 81 + 144
= 225
∴ AD2 = 225
⇒ AD = 15 cm
We know that the opposite sides of a rectangle are equal
AD = BC = 15 cm
Area of the shaded region = Area of rectangle − Area of triangle AED + Area of semicircle
\[= AB \times BC - \frac{1}{2} \times AE \times DE + \frac{1}{2}\pi \left( \frac{BC}{2} \right)^2 \]
\[ = 20 \times 15 - \frac{1}{2} \times 9 \times 12 + \frac{1}{2} \times \frac{22}{7} \times \left( \frac{15}{2} \right)^2 \]
\[ = 300 - 54 + 88 . 3928\]
\[ = 334 . 3928 {cm}^2\]
Hence, the area of shaded region is 334.39 cm2
APPEARS IN
संबंधित प्रश्न
The area of a rectangular plot is ` 462m^2` and is length is 28 m. Find its perimeter.
Find the length of the diagonal of a square whose area is `128 cm^2` Also, find its perimeter.
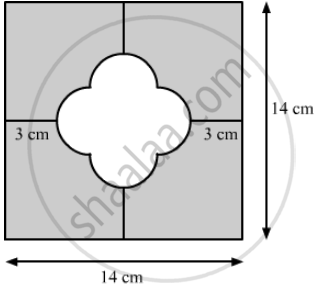
In the following figure find the area of the shaded region. (Use π = 3.14)
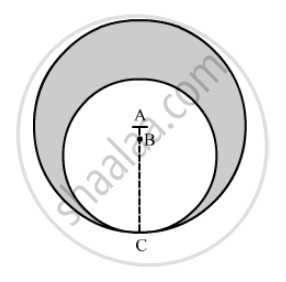
In the following figure, two circles with centres A and B touch each other at the point C. If AC = 8 cm and AB = 3 cm, find the area of the shaded region.
Write the area of the sector of a circle whose radius is r and length of the arc is l.
What is the area of a sector of a circle of radius 5 cm formed by an arc of length 3.5 cm?
The area of incircle of an equilateral triangle is 154 cm2 . The perimeter of the triangle is
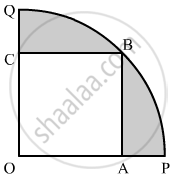
In the given figure, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. [Use π = 3.14.]
In the given figure, ABCD is a rectangle with AB = 80 cm and BC = 70 cm, ∠AED = 90° and DE = 42 cm. A semicircle is drawn, taking BC as diameter. Find the area of the shaded region.
If radius of a circle is increased to twice its original length, how much will the area of the circle increase?
