Advertisements
Advertisements
प्रश्न
If radius of a circle is increased to twice its original length, how much will the area of the circle increase?
पर्याय
1.4 times
2 times
3 times
4 times
उत्तर
4 times
Explanation:
Let r be the radius of the circle
∴ Area of circle = π2
If radius is increased to twice its original length, then radius will be 2r
Now, area of new circle = π(2r)2 = 4π2 = 4 times of original area
Hence, the area of circle will be increased by 4 times.
APPEARS IN
संबंधित प्रश्न
Find the area of the following circle, given that radius = 14 mm (take `pi = 22/7`).
From a circular piece of cardboard of radius 3 cm two sectors of 900 have been cutoff . Find the perimeter of the remaining portion nearest hundredth centimeters ( `"Take" pi = 22/ 7`).
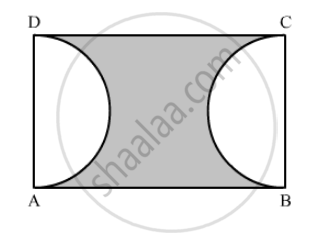
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the area of the shaded region.
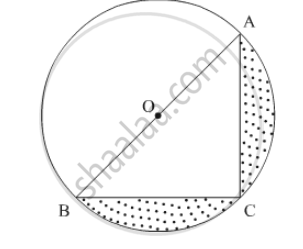
Find the area of the shaded region in the following figure, if AC = 24 cm, BC = 10 cm and O is the centre of the circle. (Use π = 3.14)
In the following figure, AB = 36 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all the three circles. Find the area of the shaded region.

The area of the largest triangle that can be inscribed in a semi-circle of radius r, is
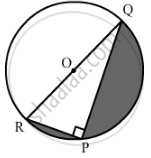
In the given figure, PQ = 24, PR = 7 cm and O is the centre of the circle. Find the area of the shaded region.
A chord of a circle of radius 10 cm subtends a right angle at the centre. The area of the minor segments (given, π = 3.14) is
The radii of the inner and outer circumferences of a circular running track are 63 m and 70 m respectively. Find :
(i) the area of the track ;
(ii) the difference between the lengths of the two circumferences of the track.
Find the area of the circle, length of whose circumference is equal to the sum of the lengths of the circumferences with radii 15 cm and 13 cm.
