Advertisements
Advertisements
प्रश्न
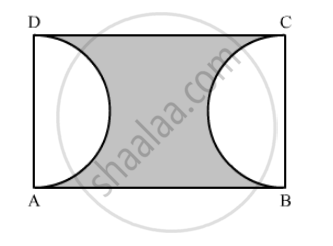
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the area of the shaded region.
उत्तर
We have given two semi-circles and a rectangle.
Area of the shaded region = Area of the rectangle − Area of the two semicircles
`∴ "Area of the shaded region" =20xx14-2xx1/2xxpixx7xx7`
Substituting pi=`22/7` we get,
`∴ "Area of the shaded region"=20xx14-2xx1/2xx22/7xx7xx7`
`∴ "Area of the shaded region"=20xx14-22xx7`
`∴ "Area of the shaded region"280-154`
`∴ "Area of the shaded region"=126`
Therefore, area of shaded region is `126 cm^2`
APPEARS IN
संबंधित प्रश्न
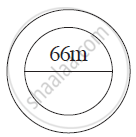
A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (π = 3.14)
The area of a parallelogram is `392m^2` . If its altitude is twice the corresponding base, determined the base and the altitude.
A square water tank has its side equal to 40 m. There are four semi-circular grassy plots all round it. Find the cost of turfing the plot at Rs. 1.25 per square metre (Take π = 3.14).
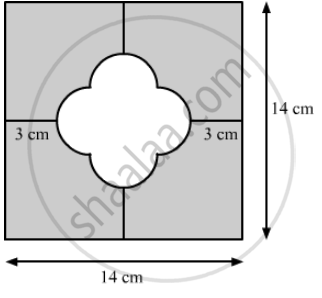
In the following figure find the area of the shaded region. (Use π = 3.14)
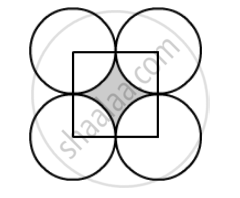
The diameter of a coin is 1 cm (in the following figure). If four such coins be placed on a table so that the rim of each touches that of the other two, find the area of the shaded region (Take π = 3.1416).
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
In the following figure, O is the centre of a circular arc and AOB is a straight line. Find the perimeter and the area of the shaded region correct to one decimal place. (Take π = 3.142)
In the following figure, ABC is an equilateral triangle of side 8 cm. A, B and C are the centres of circular arcs of radius 4 cm. Find the area of the shaded region correct upto 2 decimal places. (Take π =3.142 and`sqrt3` = 1.732).

Write the formula for the area of a segment in a circle of radius r given that the sector angle is \[\theta\] (in degrees).
Diameter of a circular garden is 9.8 m. Find its area.
