Advertisements
Advertisements
प्रश्न
In the following figure find the area of the shaded region. (Use π = 3.14)
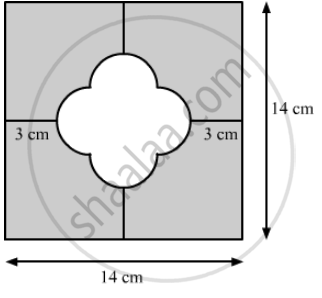
उत्तर
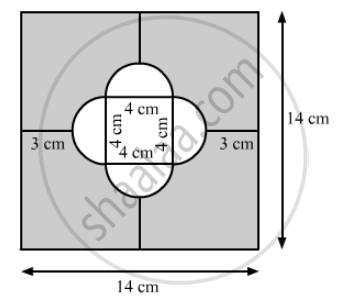
Area of shaded region = Area of square − Area of 4 semicircle having diameter 4 cm − Area of square having side 4 cm
\[= \left( Side \right)^2 - 4 \times \frac{1}{2}\pi r^2 - \left( side \right)^2 \]
\[ = \left( 14 \right)^2 - 2 \times 3 . 14 \times \left( \frac{4}{2} \right)^2 - 4^2 \]
\[ = 196 - 25 . 12 - 16\]
\[ = 154 . 88 {cm}^2\]
Hence, the area of shaded region is 154.88 cm2
APPEARS IN
संबंधित प्रश्न
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. `[\text{Use}pi=22/7]`
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm. Find the area of the sector of the circle formed by chord AB.
The area of the incircle of an equilateral triangle of side 42 cm is
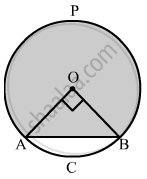
Find the area of the major segment APB of a circle of radius 35 cm and ∠AOB = 90°, as shown in the given figure.
Find the area of a ring whose outer and inner radii are respectively 23 cm and 12 cm.
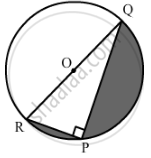
In the given figure, PQ = 24, PR = 7 cm and O is the centre of the circle. Find the area of the shaded region.
The area of circle is equal to the sum of the areas of two circles of radii 24 cm and 7 cm. The diameter of the new circle is
The length of the minute hand of a clock is 21 cm. The area swept by the minute hand in 10 minutes is
Two circles touch each other externally. The sum of their areas is 58π cm2 and the distance between their centers is 10 cm. Find the radii of the two circles.
The diameter of a wheel is 0.70 m. Find the distance covered by it in 500 revolutions. If the wheel takes 5 minutes to make 500 revolutions; find its speed in :
(i) m/s
(ii) km/hr.
