Advertisements
Advertisements
प्रश्न
In the following figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the (i) quadrant OACB (ii) shaded region.

उत्तर
It is given that OACB is a quadrant of circle with centre at O and radius 3.5 cm.
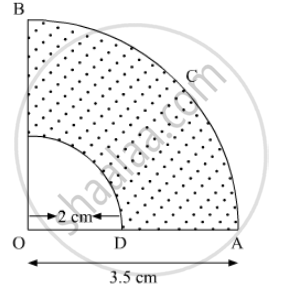
(i) We know that the area of quadrant of circle of radius r is,
`A=1/4pir^2`
Substituting the value of radius,`r=3.5 cm^2`
`A=1/4xx22/7xx3.5xx3.5`
`=9.625 cm^2`
Hence, the area of OACB is`.9.625cm^2`
(ii) It is given that radius of quadrant of small circle is 2 cm.
Let the area of quadrant of small circle be .A'
`A'1/4 pir^2`
`=1/4xx22/7xx2xx2`
`=3.14 cm^2`
It is clear from the above figure that area of shaded region is the difference of larger quadrant and the smaller one. Hence,
Area of shaded region=A-A'
`=9.625-3.14`
`= 6.485 cm^2`
APPEARS IN
संबंधित प्रश्न
Find the area and perimeter of a square plot of land whose diagonal is 24 m long.
A path of width 3.5 m runs around a semi-circular grassy plot whose perimeter is 72 m . Find the area of the path .
`("Use" pi= 22/7) `
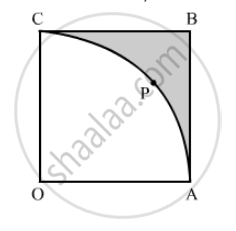
In the following figure, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. (Use π = 22/7)
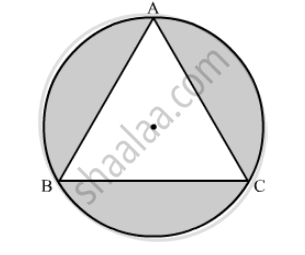
In the following figure, an equilateral triangle ABC of side 6 cm has been inscribed in a circle. Find the area of the shaded region. (Take π = 3.14).
The ratio of the outer and inner perimeters of a circular path is 23 : 22. If the path is 5 metres wide, the diameter of the inner circle is
If the area of a square is same as the area of a circle, then the ratio of their perimeters, in terms of π, is
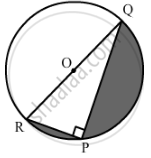
In the given figure, PQ = 24, PR = 7 cm and O is the centre of the circle. Find the area of the shaded region.
The wheel of a cart is making 5 revolutions per second. If the diameter of the wheel is 84 cm, find its speed in km per hour.
Find the length of the rope by which a bull must be tethered in order that it may be able to graze an area of 2464 m2
If radius of a circle is increased to twice its original length, how much will the area of the circle increase?
