Advertisements
Advertisements
प्रश्न
If the area of a square is same as the area of a circle, then the ratio of their perimeters, in terms of π, is
पर्याय
π :\[\sqrt{3}\]
2 : \[\sqrt{\pi}\]
3 :\[\pi\]
\[\pi : \sqrt{2}\]
उत्तर
We have given that area of a circle of radius r is equal to the area of a square of side a.
`∴ pir^2=a^2`
`∴ a=sqrtpir`
We have to find the ratio of the perimeters of circle and square.
`∴ "perimeter of circle"/"Perimeter oof square"=(2pi r)/(4a)` ..................(1)
Now we will substitute `a=sqrtpir` in equation (1)
`∴ "perimeter of circle"/"Perimeter oof square"=(2pi r)/(4sqrtr)`
`∴ "perimeter of circle"/"Perimeter oof square"=pi/(2sqrtpi)`
`∴ "perimeter of circle"/"Perimeter oof square"=sqrtpi/2`
Therefore, ratio of their perimeters is `sqrtpi:2`
APPEARS IN
संबंधित प्रश्न
A 80 m by 64 m rectangular lawn has two roads, each 5 m wide, running through its middle, one parallel to its length and the other parallel to its breadth. Find the cost of gravelling the reads at ₹` 40 per m^2`
A chord PQ of length 12 cm subtends an angle of 120° at the centre of a circle. Find the area of the minor segment cut off by the chord PQ.
Write the area of the sector of a circle whose radius is r and length of the arc is l.
The area of the largest triangle that can be inscribed in a semi-circle of radius r is
The area of a circle is 98.56 cm2. Find its circumference.
The following figure shows a square cardboard ABCD of side 28 cm. Four identical circles of the largest possible sizes are cut from this card as shown below.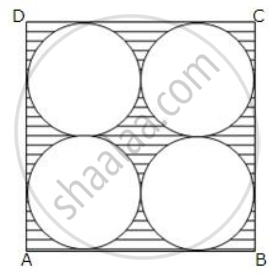
Find the area of the remaining card-board.
Find the radius and circumference of a circle, whose area is :
(i) 154 cm2
(ii) 6.16 m2
Is the area of the circle inscribed in a square of side a cm, πa2 cm2? Give reasons for your answer.
In figure, AB is a diameter of the circle, AC = 6 cm and BC = 8 cm. Find the area of the shaded region (Use π = 3.14).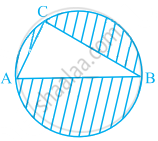
Area of a rectangle and the area of a circle are equal. If the dimensions of the rectangle are 14 cm × 11 cm, then radius of the circle is ______.
