Advertisements
Advertisements
प्रश्न
In figure, AB is a diameter of the circle, AC = 6 cm and BC = 8 cm. Find the area of the shaded region (Use π = 3.14).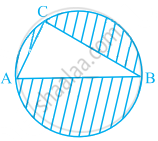
उत्तर
Given, AC = 6 cm and BC = 8 cm
We know that, triangle in a semi-circle with hypotenuse as diameter is right angled triangle.
∴ ∠C = 90°
In right angled ΔACB, use Pythagoras theorem,
∴ AB2 = AC2 + CB2
⇒ AB2 = 62 + 82
⇒ AB2 = 36 + 64
⇒ AB2 = 100
⇒ AB = 10 cm ...[Since, side cannot be negative]
∴ Area of ΔABC =
=
= 24 cm2
Here, diameter of circle,
AB = 10 cm
∴ Radius of circle,
r =
Area of circle = πr2
= 3.14 × (5)2
= 3.14 × 25
= 78.5 cm2
∴ Area of the shaded region = Area of circle – Area of ΔABC
= 78.5 – 24
= 54.5 cm2
APPEARS IN
संबंधित प्रश्न
A circular flower garden has an area of 314 m2. A sprinkler at the centre of the garden can cover an area that has a radius of 12 m. Will the sprinkler water the entire garden? (Take π = 3.14)
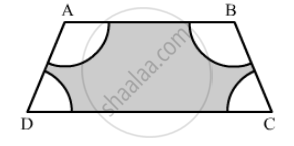
In the given figure, ABCD is a trapezium with AB || DC, AB = 18 cm DC = 32 cm and the distance between AB and DC is 14 cm. Circles of equal radii 7 cm with centres A, B, C and D have been drawn. Then find the area of the shaded region.
(Use
The area of a sector whose perimeter is four times its radius r units, is
Find the lengths of the arcs cut off from a circle of radius 12 cm by a chord 12 cm long. Also, find the area of the minor segment.
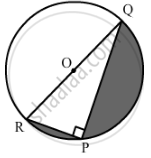
In the given figure, PQ = 24, PR = 7 cm and O is the centre of the circle. Find the area of the shaded region.
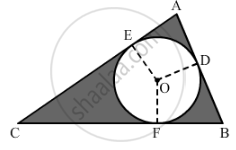
In the given figure, ∆ABC is right-angled at A. Find the area of the shaded region if AB = 6 cm, BC = 10 cm and O is the centre of the incircle of ∆ABC.
The following figure shows a square cardboard ABCD of side 28 cm. Four identical circles of the largest possible sizes are cut from this card as shown below.
Find the area of the remaining card-board.
A circular field of radius 105 m has a circular path of uniform width of 5 m along and inside its boundary. Find the area of the path.
Thenmozhi wants to level her circular flower garden whose diameter is 49 m at the rate of ₹ 150 per m2 Find the cost of levelling
What is the diameter of a circle whose area is equal to the sum of the areas of two circles of radii 40cm and 9cm?
