Advertisements
Advertisements
प्रश्न
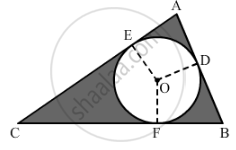
In the given figure, ∆ABC is right-angled at A. Find the area of the shaded region if AB = 6 cm, BC = 10 cm and O is the centre of the incircle of ∆ABC.
उत्तर
Using Pythagoras' theorem for triangle ABC, we have:
CA2 + AB2 = BC2
CA` = sqrt("BC"^2 - "AB"^2)`
`=sqrt(100-36)`
`=sqrt(64)`
= 8 cm
Now, we must find the radius of the incircle. Draw OE, OD and OF perpendicular to AC, AB and BC, respectively.
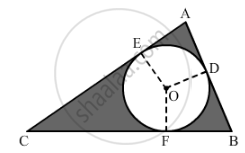
Consider quadrilateral AEOD.
Here,
EO = OD(Both are radii.)
Because the circle is an incircle, AE and AD are tangents to the circle.
∠AEO = ∠ADO = 90°
Also,
∠A = 90°
Therefore, AEOD is a square.
Thus, we can say that AE = EO = OD = AD = r.
CE = CF = 8 - r
BF = BD = 6 - r
CF + BF = 10
⇒ (8 - r)+(6-r) = 10
⇒ 14 - 2r = 10
⇒ r = 2 cm
Area of the shaded part = Area of the triangle-- Area of the circle
`= {1/2xx6xx8} - {pixx2xx2}`
= 24 - 12.56
= 11.44 cm2
APPEARS IN
संबंधित प्रश्न
A rectangular park 358 m long and 18 m wide is to be covered with grass, leaving 2.5 m uncovered all around it. Find the area to be laid with grass.
The cost of painting the four walls of a room 12 m long at `₹ 30 per m^2 is ₹ 7560 per m^2` and the cost of covering the floor with the mat at ₹` 25 per m^2 is ₹ 2700 `. find the dimensions of the room.
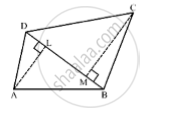
In the given figure ABCD is quadrilateral in which diagonal BD = 24 cm, AL ⊥ BD and CM ⊥ BD such that AL = 9cm and CM = 12 cm. Calculate the area of the quadrilateral.
Find the area of a parallelogram with base equal to 25 cm and the corresponding height measuring 16.8 cm.
In the following figure, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. (Use π = 22/7)
Find the area of a shaded region in the the following figure,where a circular arc of radius 7 cm has been drawn with vertex A of an equilateral triangle ABC of side 14 cm as centre. (Use π = 22/7 and \[\sqrt{3}\] = 1.73)
The short and long hands of a clock are 4 cm and 6 cm long respectively. Find the sum of distances travelled by their tips in 2 days.
A chord of a circle of radius 14 cm a makes a right angle at the centre. Find the area of the sector.
The radii of two circles are in the ratio 3: 8. If the difference between their areas is 2695π cm2, find the area of the smaller circle.
The diameters of three wheels are in the ratio 2 : 4 : 8. If the sum of the circumferences of these circles be 132 cm, find the difference between the areas of the largest and the smallest of these wheels.
