Advertisements
Advertisements
Question
In the given figure, ∆ABC is right-angled at A. Find the area of the shaded region if AB = 6 cm, BC = 10 cm and O is the centre of the incircle of ∆ABC.
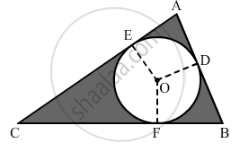
Solution
Using Pythagoras' theorem for triangle ABC, we have:
CA2 + AB2 = BC2
CA` = sqrt("BC"^2 - "AB"^2)`
`=sqrt(100-36)`
`=sqrt(64)`
= 8 cm
Now, we must find the radius of the incircle. Draw OE, OD and OF perpendicular to AC, AB and BC, respectively.
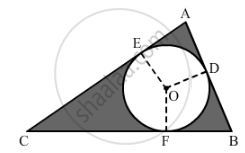
Consider quadrilateral AEOD.
Here,
EO = OD(Both are radii.)
Because the circle is an incircle, AE and AD are tangents to the circle.
∠AEO = ∠ADO = 90°
Also,
∠A = 90°
Therefore, AEOD is a square.
Thus, we can say that AE = EO = OD = AD = r.
CE = CF = 8 - r
BF = BD = 6 - r
CF + BF = 10
⇒ (8 - r)+(6-r) = 10
⇒ 14 - 2r = 10
⇒ r = 2 cm
Area of the shaded part = Area of the triangle-- Area of the circle
`= {1/2xx6xx8} - {pixx2xx2}`
= 24 - 12.56
= 11.44 cm2
APPEARS IN
RELATED QUESTIONS
A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (π = 3.14)
Find the length of the hypotenuse of an isosceles right-angled triangle whose area is `200^2` cm . Also, find its perimeter
A room is 16 m long and 13.5 m broad. Find the cost of covering its floor with 75-m-wide carpet at ₹ 60 per metre.
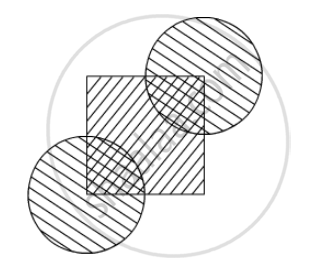
In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O' are centres of the circles. Find the area of shaded region.
The perimeter of the sector OAB shown in the following figure, is

Area of the largest triangle that can be inscribed in a semi-circle of radius r units is ______.
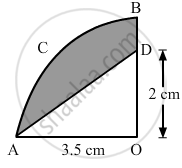
In the given figure, OABC is a quadrant of a circle of radius 3.5 cm with centre O. If OD = 2 cm, find the area of the shaded portion.
A square is inscribed in a circle of radius 6 cm. Find the area of the square. Give your answer correct to two decimal places if `sqrt(2)` = 1.414.
Calculate the area of the shotput circle whose radius is 2.135 m.
The floor of the circular swimming pool whose radius is 7 m has to be cemented at the rate of ₹ 18 per m2. Find the total cost of cementing the floor
