Advertisements
Advertisements
Question
Area of the largest triangle that can be inscribed in a semi-circle of radius r units is ______.
Options
r2 sq.units
r2
2r2
`1/2 "r"^2` sq.units
2r2 sq.units
r3
`sqrt(2)"r"^2` sq.units
2r3
Solution
Area of the largest triangle that can be inscribed in a semi-circle of radius r units is r2 sq.units.
Explanation:
The largest triangle that can be inscribed in a semi-circle of radius r units is the triangle having its base as the diameter of the semi-circle and the two other sides are taken by considering a point C on the circumference of the semi-circle and joining it by the endpoints of diameter A and B.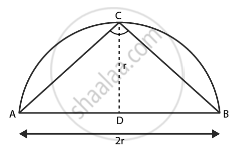
∴ ∠C = 90° ...(By the properties of circle)
So, ΔABC is right-angled triangle with base as diameter AB of the circle and height be CD.
Height of the triangle = r
∴ Area of largest ΔABC = `1/2 xx "Base" xx "Height"`
= `1/2 xx "AB" xx "CD"`
= `1/2 xx 2"r" xx "r"`
= r2 sq.units
RELATED QUESTIONS
A circular flower garden has an area of 314 m2. A sprinkler at the centre of the garden can cover an area that has a radius of 12 m. Will the sprinkler water the entire garden? (Take π = 3.14)
In the following figure, the square ABCD is divided into five equal parts, all having same area. The central part is circular and the lines AE, GC, BF and HD lie along the diagonals AC and BD of the square. If AB = 22 cm, find:
the perimeter of the part ABEF.

In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the perimeter of the cross-section
If the circumference of two circles are in the ratio 2 : 3, what is the ratio of their areas?
If the adjoining figure is a sector of a circle of radius 10.5 cm, what is the perimeter of the sector? (Take \[\pi = 22/7\])
How many revolutions a circular wheel of radius r metres makes in covering a distance of s metres?
In the following figure, the area of the segment PAQ is

A horse is tethered to one corner of a field which is in the shape of an equilateral triangle of side 12 m. If the length of the rope is 7 m, find the area of the field which the horse cannot graze. Write the answer correct to 2 places of decimal.
The following figure shows a square cardboard ABCD of side 28 cm. Four identical circles of the largest possible sizes are cut from this card as shown below.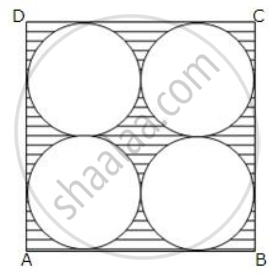
Find the area of the remaining card-board.
Find the area of a ring-shaped region enclosed between two concentric circles of radii 20 cm and 15 cm.
