Advertisements
Advertisements
Question
If the sum of the areas of two circles with radii R1 and R2 is equal to the area of a circle of radius R, then ______.
Options
R1 + R2 = R
`"R"_1^2 + "R"_2^2 = "R"^2`
R1 + R2 < R
`"R"_1^2 + "R"_2^2 < "R"^2`
Solution
If the sum of the areas of two circles with radii R1 and R2 is equal to the area of a circle of radius R, then `underlinebb("R"_1^2 + "R"_2^2 = "R"^2)`.
Explanation:
According to the question,
Area of circle = Area of first circle + Area of second circle
∴ `π"R"^2 = π"R"_1^2 + π"R"_2^2`
⇒ `"R"^2 = "R"_1^2 + "R"_2^2`
RELATED QUESTIONS
Find the area of the following circle, given that diameter = 49 m.
Find the length of the hypotenuse of an isosceles right-angled triangle whose area is `200^2` cm . Also, find its perimeter
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. `[\text{Use}pi=22/7]`
Find the area of a shaded region in the the following figure,where a circular arc of radius 7 cm has been drawn with vertex A of an equilateral triangle ABC of side 14 cm as centre. (Use π = 22/7 and \[\sqrt{3}\] = 1.73)
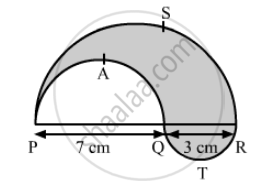
In the the following figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region.
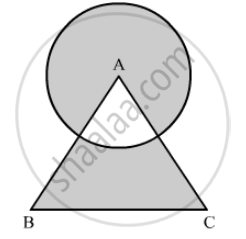
In the following figure, two circles with centres A and B touch each other at the point C. If AC = 8 cm and AB = 3 cm, find the area of the shaded region.

The area of the largest triangle that can be inscribed in a semi-circle of radius r, is
Find the areas of both the segments of a circle of radius 42 cm with central angle 120°.
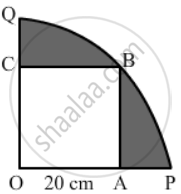
In the given figure, a square OABC has been inscribed in the quadrant OPBQ. If OA = 20 cm, then the area of the shaded region is
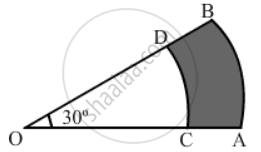
In the given figure, the sectors of two concentric circles of radii 7 cm and 3.5 cm are shown. Find the area of the shaded region.