Advertisements
Advertisements
प्रश्न
Area of the largest triangle that can be inscribed in a semi-circle of radius r units is ______.
पर्याय
r2 sq.units
r2
2r2
`1/2 "r"^2` sq.units
2r2 sq.units
r3
`sqrt(2)"r"^2` sq.units
2r3
उत्तर
Area of the largest triangle that can be inscribed in a semi-circle of radius r units is r2 sq.units.
Explanation:
The largest triangle that can be inscribed in a semi-circle of radius r units is the triangle having its base as the diameter of the semi-circle and the two other sides are taken by considering a point C on the circumference of the semi-circle and joining it by the endpoints of diameter A and B.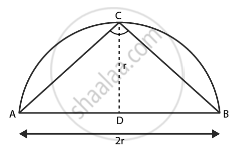
∴ ∠C = 90° ...(By the properties of circle)
So, ΔABC is right-angled triangle with base as diameter AB of the circle and height be CD.
Height of the triangle = r
∴ Area of largest ΔABC = `1/2 xx "Base" xx "Height"`
= `1/2 xx "AB" xx "CD"`
= `1/2 xx 2"r" xx "r"`
= r2 sq.units
संबंधित प्रश्न
Find the area of the following circle, given that diameter = 49 m.
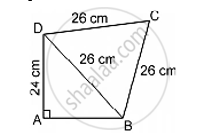
Find the area of the quadrilateral ABCD in which AD = 24 cm, ∠BAD 90° and ∠BCD is an equilateral triangle having each side equal to 26 cm. Also, find the perimeter of the quadrilateral.
Prove that the area of a circular path of uniform width h surrounding a circular region of radius r is `pih(2r+h)`
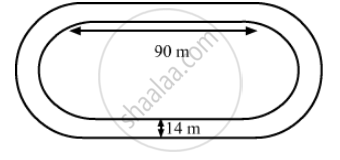
The inside perimeter of a running track (shown in the following figure) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If the track is everywhere 14 m wide. find the area of the track. Also find the length of the outer running track.
A regular hexagon is inscribed in a circle. If the area of hexagon is \[24\sqrt{3}\] , find the area of the circle. (Use π = 3.14)
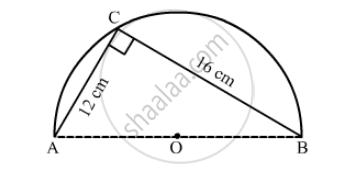
In the following figure, O is the centre of a circular arc and AOB is a straight line. Find the perimeter and the area of the shaded region correct to one decimal place. (Take π = 3.142)
If the area of a square is same as the area of a circle, then the ratio of their perimeters, in terms of π, is
A square tank has an area of 1600 cm2. There are four semicircular plots around it. Find the cost of turfing the plots at Rs 12.50 per m2
The area of the circle is 154 cm2. The radius of the circle is ______.
The area of the circle whose diameter is 21 cm is ____________.
