Advertisements
Advertisements
प्रश्न
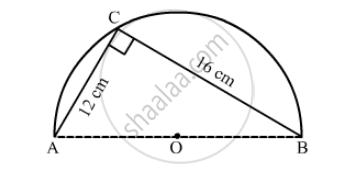
In the following figure, O is the centre of a circular arc and AOB is a straight line. Find the perimeter and the area of the shaded region correct to one decimal place. (Take π = 3.142)
उत्तर
(i) Let us find the perimeter of the shaded region.
`∴ "Perimeter"=pixx10+12+16`
`∴ "Perimeter"=3.142xx10+28`
`∴ "Perimeter"=31.42+28`
`∴ "Perimeter"=59.42`
Therefore, perimeter of the shaded region is 59.4cm.
Now we will find the area of the shaded region can be calculated as shown below,Area of the shaded region = Area of the semi-circle − area of the right angled triangle First, we will find the length of AB as shown below,
`AB^2=AC^2+CB^2`
`∴ AB^2=12^2+16^2`
`∴ AB^2=144+256`
`∴ AB^2=400`
`∴AB^2=20`
`∴"Area of the shaded region" =(pixx10xx10)/2-1/2xx12xx16`
`∴"Area of the shaded region"=pixx50-6xx16`
`∴"Area of the shaded region"= pixx50-96`
Substituting pi=3.142 we get,
`∴"Area of the shaded region"=3.142xx50-96`
`∴"Area of the shaded region"=157.1-96`
`∴"Area of the shaded region"=61.1`
Therefore, area of the shaded region is `61.1 cm^2`
APPEARS IN
संबंधित प्रश्न
In the following figure, there are three semicircles, A, B and C having diameter 3 cm each, and another semicircle E having a circle D with diameter 4.5 cm are shown. Calculate:
(i) the area of the shaded region
(ii) the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.

Write the formula for the area of a segment in a circle of radius r given that the sector angle is \[\theta\] (in degrees).
The area of a circular path of uniform width h surrounding a circular region of radius r is
If a chord of a circle of radius 28 cm makes an angle of 90 ° at the centre, then the area of the major segment is
Two circles touch each other externally. The sum of their areas is 58π cm2 and the distance between their centers is 10 cm. Find the radii of the two circles.
If a square in inscribed in a circle, find the ratio of the areas of the circle and the square.
The circumference of a circular table is 88 m. Find its area.
Find the area of the biggest circle that can be cut from a rectangular piece 44cm by 28cm. also, find the area of the paper left after cutting out the circle.
The area (in cm2) of the circle that can be inscribed in a square of side 8 cm is ____________.
The length of the minute hand of a clock is 14 cm. The area swept by the minute hand in 5 minutes is ______.
