Advertisements
Advertisements
Question
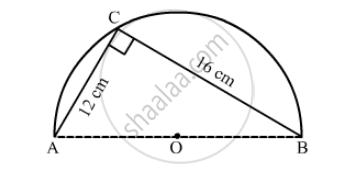
In the following figure, O is the centre of a circular arc and AOB is a straight line. Find the perimeter and the area of the shaded region correct to one decimal place. (Take π = 3.142)
Solution
(i) Let us find the perimeter of the shaded region.
`∴ "Perimeter"=pixx10+12+16`
`∴ "Perimeter"=3.142xx10+28`
`∴ "Perimeter"=31.42+28`
`∴ "Perimeter"=59.42`
Therefore, perimeter of the shaded region is 59.4cm.
Now we will find the area of the shaded region can be calculated as shown below,Area of the shaded region = Area of the semi-circle − area of the right angled triangle First, we will find the length of AB as shown below,
`AB^2=AC^2+CB^2`
`∴ AB^2=12^2+16^2`
`∴ AB^2=144+256`
`∴ AB^2=400`
`∴AB^2=20`
`∴"Area of the shaded region" =(pixx10xx10)/2-1/2xx12xx16`
`∴"Area of the shaded region"=pixx50-6xx16`
`∴"Area of the shaded region"= pixx50-96`
Substituting pi=3.142 we get,
`∴"Area of the shaded region"=3.142xx50-96`
`∴"Area of the shaded region"=157.1-96`
`∴"Area of the shaded region"=61.1`
Therefore, area of the shaded region is `61.1 cm^2`
APPEARS IN
RELATED QUESTIONS
A 80 m by 64 m rectangular lawn has two roads, each 5 m wide, running through its middle, one parallel to its length and the other parallel to its breadth. Find the cost of gravelling the reads at ₹` 40 per m^2`
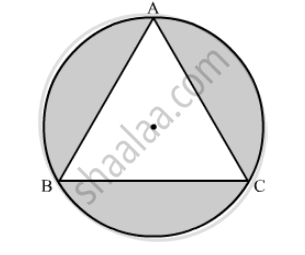
In the following figure, an equilateral triangle ABC of side 6 cm has been inscribed in a circle. Find the area of the shaded region. (Take π = 3.14).
What is the angle subtended at the centre of a circle of radius 6 cm by an arc of length 3 π cm?
If a chord of a circle of radius 28 cm makes an angle of 90 ° at the centre, then the area of the major segment is
The hour hand of a clock is 6 cm long. The area swept by it between 11.20 am and 11.55 am is
A square is inscribed in a circle. Find the ratio of the areas of the circle and the square.
The area of a circle is 98.56 cm2. Find its circumference.
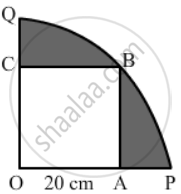
In the given figure, a square OABC has been inscribed in the quadrant OPBQ. If OA = 20 cm, then the area of the shaded region is
A chord of a circle of radius 14 cm a makes a right angle at the centre. Find the area of the sector.
Find the area of the shaded portion in each of the following diagrams:
(i)

(ii)

