Advertisements
Advertisements
Question
A square is inscribed in a circle. Find the ratio of the areas of the circle and the square.
Solution
Let the side of the square be a and radius of the circle be r
We know that if a circle circumscribes a square, then the diameter of the circle is equal to the diagonal of the square.
`∴ sqrt(2a) = 2r`
`⇒ a = sqrt(2r)`
Now ,
`"Area of circle"/"Area of square" = (pi"r"^2)/"a"^2`
`= (pi"r"^2)/(sqrt(2r))^2`
`= ( pi"r"^2)/(2pi^2)`
`= pi/2`
Hence, the ratio of the areas of the circle and the square is π : 2
APPEARS IN
RELATED QUESTIONS
A footpath of uniform width runs all around the inside of a rectangular field 54m long and 35 m wide. If the area of the path is `420m^2` , find the width of the path.
Prove that the area of a circular path of uniform width h surrounding a circular region of radius r is `pih(2r+h)`
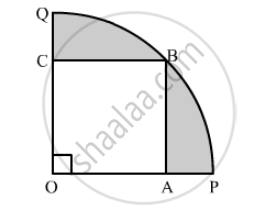
In the following figure a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 21 cm, find the area of the shaded region.
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
In the following figure, the shaded area is

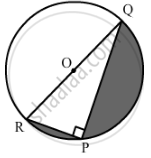
In the given figure, PQ = 24, PR = 7 cm and O is the centre of the circle. Find the area of the shaded region.
A chord of a circle of radius 10 cm subtends a right angle at the centre. The area of the minor segments (given, π = 3.14) is
The diameters of three circles are in the ratio 3: 5: 6. If the sum of the circumferences of these circles is 308 cm; find the difference between the areas of the largest and the smallest of these circles.
The area of a circle is 1386 sq.cm; find its circumference.
A wire, when bent in the form of a square; encloses an area of 196 cm2. If the same wire is bent to form a circle; find the area of the circle.
