Advertisements
Advertisements
Question
A wire, when bent in the form of a square; encloses an area of 196 cm2. If the same wire is bent to form a circle; find the area of the circle.
Solution
Area of Square = 196 cm2
Side of Square = `sqrt("Area")` = `sqrt(196)` = 14 cm
Perimeter of Square = 4 x 14 cm
i.e. length of wire = 56 cm
Circumference of circle = 56 cm
2πr = 56
`2 xx 22/7 xx r = 56`
`r = (56 xx 7)/(2 xx 22)`
`r = 98/11` cm
`therefore "Area of circle enclosed" = pir^2`
= `22/7 xx 98/11 xx 98/11`
= `2744/11`
= 249.45 cm2
APPEARS IN
RELATED QUESTIONS
In the given figure, ΔABC is an equilateral triangle the length of whose side is equal to 10 cm, and ΔADC is right-angled at D and BD= 8cm. Find the area of the shaded region.

The area of a parallelogram is `392m^2` . If its altitude is twice the corresponding base, determined the base and the altitude.
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. `[\text{Use}pi=22/7]`
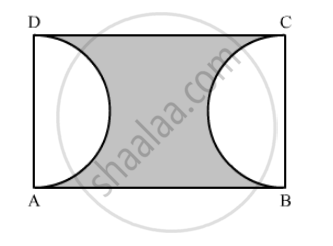
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the area of the shaded region.
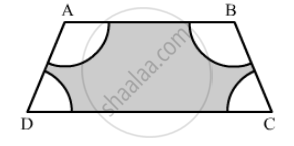
In the given figure, ABCD is a trapezium with AB || DC, AB = 18 cm DC = 32 cm and the distance between AB and DC is 14 cm. Circles of equal radii 7 cm with centres A, B, C and D have been drawn. Then find the area of the shaded region.
(Use \[\pi = \frac{22}{7}\]
What is the diameter of a circle whose area is equal to the sum of the areas of two circles of diameters 10 cm and 24 cm?
A square is inscribed in a circle of radius 7 cm. Find the area of the square.
The diameters of three wheels are in the ratio 2 : 4 : 8. If the sum of the circumferences of these circles be 132 cm, find the difference between the areas of the largest and the smallest of these wheels.
A 7m wide road surrounds a circular garden whose area is 5544m2. Find the area of the road and the cost of tarring it at the rate of Rs.150 per m2.
On a square cardboard sheet of area 784 cm2, four congruent circular plates of maximum size are placed such that each circular plate touches the other two plates and each side of the square sheet is tangent to two circular plates. Find the area of the square sheet not covered by the circular plates.
