Advertisements
Advertisements
Question
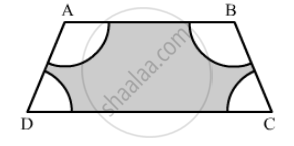
In the given figure, ABCD is a trapezium with AB || DC, AB = 18 cm DC = 32 cm and the distance between AB and DC is 14 cm. Circles of equal radii 7 cm with centres A, B, C and D have been drawn. Then find the area of the shaded region.
(Use \[\pi = \frac{22}{7}\]
Solution
Area of shaded region = Area of trapezium ABCD − Area of 4 sectors
\[= \frac{1}{2}\left( AB + DC \right) \times 14 - \left( \frac{\angle A}{360°}\pi r^2 + \frac{\angle B}{360°}\pi r^2 + \frac{\angle C}{360°}\pi r^2 + \frac{\angle D}{360°}\pi r^2 \right)\]
\[ = \frac{1}{2}\left( AB + DC \right) \times 14 - \left( \frac{\angle A + \angle B + \angle C + \angle D}{360°} \right)\pi r^2 \]
\[ = \frac{1}{2}\left( 18 + 32 \right) \times 14 - \frac{22}{7} \left( 7 \right)^2 \]
\[ = 350 - 154\]
\[ = 196 {cm}^2\]
Hence, the area of shaded region is 196 cm2
APPEARS IN
RELATED QUESTIONS
The cost of harvesting a square field at ₹ 900 per hectare is ₹ 8100. Find the cost of putting a fence around it at ₹ 18 per meter.
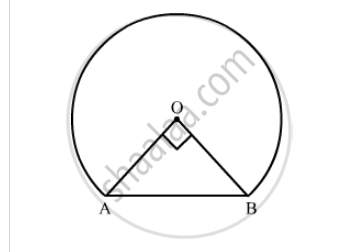
In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the height of the tunnel
In a hospital used water is collected in a cylindrical tank of diameter 2 m and height 5 m. After recycling, this water is used to irrigate a park of hospital whose length is 25 m and breadth is 20 m. If tank is filled completely then what will be the height of standing water used for irrigating the park.
If a chord of a circle of radius 28 cm makes an angle of 90 ° at the centre, then the area of the major segment is
From a rectangular sheet of paper ABCD with AB = 40 cm and AD = 28 cm, a semicircular portion with BC as diameter is cut off. Find the area of the remaining paper.
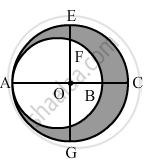
In the given figure, O is the centre of the bigger circle, and AC is its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10, find the area of the shaded region.
The area of circle is equal to the sum of the areas of two circles of radii 24 cm and 7 cm. The diameter of the new circle is
Find the radius and area of a circle, whose circumference is :
(i) 132 cm
(ii) 22 m
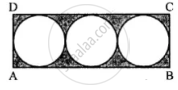
In the following figure, a rectangle ABCD enclosed three circles. If BC = 14 cm, find the area of the shaded portion (Take π = 22/7)
The area of the circular ring enclosed between two concentric circles is 88 cm2. Find the radii of the two circles, if their difference is 1 cm.
