Advertisements
Advertisements
Question
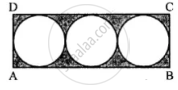
In the following figure, a rectangle ABCD enclosed three circles. If BC = 14 cm, find the area of the shaded portion (Take π = 22/7)
Solution
To calculate the area of the shaded portion, we need to subtract the total area of the three circles from the area of the rectangle.
- Length of BC (Rectangle's width): 14 cm
- The three circles are identical, and their diameters fit perfectly along the length of the rectangle (AD).
Thus: Diameter of each circle = `("Length of AD (Rectangle)")/("Number of circles")"`
`= 14/3 = 14/3 cm`
Radius of each circle = `"Diameter"/2 = 14/6 = 7/3 cm`
Step 1: Area of the rectangle
Area of Rectangle = Length × Width = AD × BC.
AD = 14 cm, BC = 14 cm.
Area of Rectangle = 14 × 14 = 96 cm2
Step 2: Total area of the three circles
Area of one circle = πr2.
`r = 7/3 cm, pi=22/7`
Area of one circle `= 22/7xx(7/3)^2=22/7xx49/9=1078/63 cm^2`
Total Area of Circles `= 3xx1078/63 = 3234/63 = 51.33 cm^2`
Step 3: Area of the shaded portion
Shaded Area = Area of Rectangle − Total Area of Circles.
Shaded Area = 196 − 51.33 = 144.67 cm2.
The area of the shaded portion is approximately: 144.67 cm2
APPEARS IN
RELATED QUESTIONS
Find the length of the diagonal of a square whose area is `128 cm^2` Also, find its perimeter.
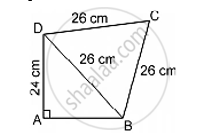
Find the area of the quadrilateral ABCD in which AD = 24 cm, ∠BAD 90° and ∠BCD is an equilateral triangle having each side equal to 26 cm. Also, find the perimeter of the quadrilateral.
A path of width 3.5 m runs around a semi-circular grassy plot whose perimeter is 72 m . Find the area of the path .
`("Use" pi= 22/7) `
How many revolutions a circular wheel of radius r metres makes in covering a distance of s metres?
If the radius of a circle is diminished by 10%, then its area is diminished by
If the area of a sector of a circle is `5/18` of the area of the circle, then the sector angle is equal to
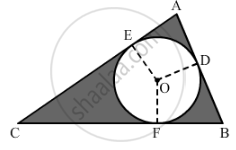
In the given figure, ∆ABC is right-angled at A. Find the area of the shaded region if AB = 6 cm, BC = 10 cm and O is the centre of the incircle of ∆ABC.
The diameters of three wheels are in the ratio 2 : 4 : 8. If the sum of the circumferences of these circles be 132 cm, find the difference between the areas of the largest and the smallest of these wheels.
If radius of a circle is increased to twice its original length, how much will the area of the circle increase?
How much distance, in metres, a wheel of 25 cm radius will cover if it rotates 350 times?
