Advertisements
Advertisements
प्रश्न
In the following figure, a rectangle ABCD enclosed three circles. If BC = 14 cm, find the area of the shaded portion (Take π = 22/7)
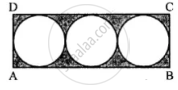
उत्तर
To calculate the area of the shaded portion, we need to subtract the total area of the three circles from the area of the rectangle.
- Length of BC (Rectangle's width): 14 cm
- The three circles are identical, and their diameters fit perfectly along the length of the rectangle (AD).
Thus: Diameter of each circle = `("Length of AD (Rectangle)")/("Number of circles")"`
`= 14/3 = 14/3 cm`
Radius of each circle = `"Diameter"/2 = 14/6 = 7/3 cm`
Step 1: Area of the rectangle
Area of Rectangle = Length × Width = AD × BC.
AD = 14 cm, BC = 14 cm.
Area of Rectangle = 14 × 14 = 96 cm2
Step 2: Total area of the three circles
Area of one circle = πr2.
`r = 7/3 cm, pi=22/7`
Area of one circle `= 22/7xx(7/3)^2=22/7xx49/9=1078/63 cm^2`
Total Area of Circles `= 3xx1078/63 = 3234/63 = 51.33 cm^2`
Step 3: Area of the shaded portion
Shaded Area = Area of Rectangle − Total Area of Circles.
Shaded Area = 196 − 51.33 = 144.67 cm2.
The area of the shaded portion is approximately: 144.67 cm2
APPEARS IN
संबंधित प्रश्न
The circumference of a circle is 31.4 cm. Find the radius and the area of the circle? (Take π = 3.14)
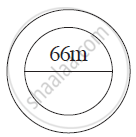
A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (π = 3.14)
Find the area of a parallelogram with base equal to 25 cm and the corresponding height measuring 16.8 cm.
Prove that the area of a circular path of uniform width h surrounding a circular region of radius r is `pih(2r+h)`
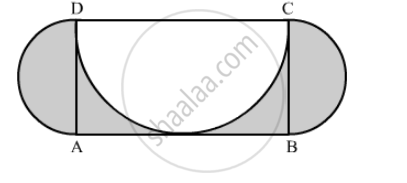
In the following figure, ABCD is a rectangle with AB = 14 cm and BC = 7 cm. Taking DC, BC and AD as diameters, three semi-circles are drawn as shown in the figure. Find the area of the shaded region.
A circular field has a perimeter of 650 m. A square plot having its vertices on the circumference of the field is marked in the field. Calculate the area of the square plot.
If the circumference of two circles are in the ratio 2 : 3, what is the ratio of their areas?
What is the length (in terms of π) of the arc that subtends an angle of 36° at the centre of a circle of radius 5 cm?
If the sum of the areas of two circles with radii R1 and R2 is equal to the area of a circle of radius R, then ______.
Area of a quadrant of a circle of radius 7 cm is ______.
