Advertisements
Advertisements
प्रश्न
If the circumference of two circles are in the ratio 2 : 3, what is the ratio of their areas?
उत्तर
We are given ratio of circumferences of two circles. If `C=2 pir` and `C'=2pi r'` are circumferences of two circles such that
`C/C'=2/3`
⇒` (2pi r)/(2pi r')=2/3` ..............(1)
Simplifying equation (1) we get,
`r/(r')=2/3`
Let `A=pir^2` and `A'=pir^('2)` are the areas of the respective circles and we are asked to find their ratio.
`A/A'=(pir^2)/(pir^('2))`
`A/A'=r^2/r^('2)`
`A/A'=(r/(r'))^2` ...................(2)
We know that `r/(r')=2/3`substituting this value in equation (2) we get,
`A/(A')=(2/3)^2`
`⇒ A/(A')=4/9`
Therefore, ratio of their areas is `4:9`
APPEARS IN
संबंधित प्रश्न
Find the area and perimeter of an isosceles right angled triangle, each of whose equal sides measure 10cm.
A rectangular park 358 m long and 18 m wide is to be covered with grass, leaving 2.5 m uncovered all around it. Find the area to be laid with grass.
The outer circumference of a circular race-track is 528 m . The track is everywhere 14 m wide. Calculate the cost of levelling the track at the rate of 50 paise per square metre.
`(use pi=22/7). `
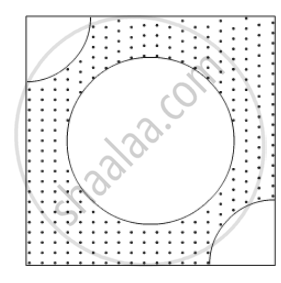
From each of the two opposite corners of a square of side 8 cm, a quadrant of a circle of radius 1.4 cm is cut. Another circle of radius 4.2 cm is also cut from the centre as shown in the following figure. Find the area of the remaining (Shaded) portion of the square. (Use π = 22/7)
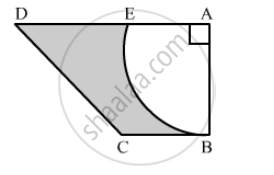
In the following figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region. [CBSE 2014]
If the perimeter of a sector of a circle of radius 6.5 cm is 29 cm, then its area is
The length of the minute hand of a clock is 21 cm. The area swept by the minute hand in 10 minutes is
In the given figure, ABCD is a square each of whose sides measures 28 cm. Find the area of the shaded region.

Find the radius and area of a circle, whose circumference is :
(i) 132 cm
(ii) 22 m
The area (in cm2) of the circle that can be inscribed in a square of side 8 cm is ____________.
