Advertisements
Advertisements
प्रश्न
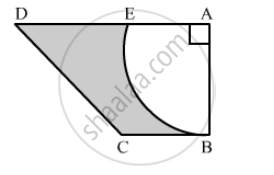
In the following figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region. [CBSE 2014]
उत्तर
Area of trapezium =\[\left( 3\pi + 2 \right) m^2\]
\[\Rightarrow 24 . 5 = \frac{1}{2}\left( 10 + 4 \right) \times AB\]
\[ \Rightarrow AB = 3 . 5 cm\]
Area of shaded region = Area of trapezium ABCD − Area of quadrant ABE
\[= 24 . 5 - \frac{1}{4} \times \frac{22}{7} \times \left( 3 . 5 \right)^2 \]
\[ = 24 . 5 - 9 . 625\]
\[ = 14 . 875 {cm}^2\]
Hence, the area of shaded region is 14.875 cm2
APPEARS IN
संबंधित प्रश्न
Find the area of the following circles, given that radius = 5 cm.
A square water tank has its side equal to 40 m. There are four semi-circular grassy plots all round it. Find the cost of turfing the plot at Rs. 1.25 per square metre (Take π = 3.14).
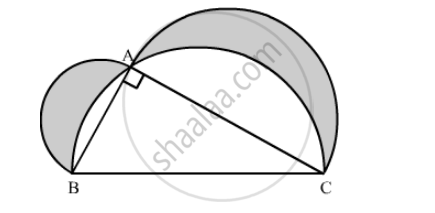
In the following figure, ABC is a right angled triangle in which ∠A = 90°, AB = 21 cm and AC = 28 cm. Semi-circles are described on AB, BC and AC as diameters. Find the area of the shaded region.
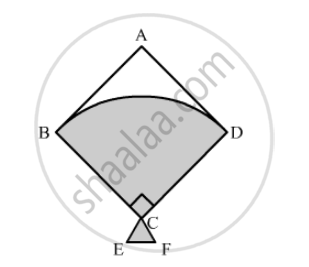
In the following figure, shows a kite in which BCD is the shape of a quadrant of a circle of radius 42 cm. ABCD is a square and Δ CEF is an isosceles right angled triangle whose equal sides are 6 cm long. Find the area of the shaded region.
What is the area of a sector of a circle of radius 5 cm formed by an arc of length 3.5 cm?
If a square is inscribed in a circle, what is the ratio of the areas of the circle and the square?
The area of the largest triangle that can be inscribed in a semi-circle of radius r is
The area of the circle that can be inscribed in a square of side 10 cm is
A square is inscribed in a circle. Find the ratio of the areas of the circle and the square.
The diameter of a wheel is 40 cm. How many revolutions will it make in covering 176 m?
