Advertisements
Advertisements
प्रश्न
The diameter of a wheel is 40 cm. How many revolutions will it make in covering 176 m?
पर्याय
140
150
160
166
उत्तर
140
Distance covered by the wheel in 1 revolutio = πd
`=(22/7xx40)"cm"`
`= 880/7 "cm"`
`=880/(7xx100) "m"`
Number of revolutions required to cover 176 m`=(176/(880/(7xx100)))`
`= (176xx100xx7/880)`
= 140
APPEARS IN
संबंधित प्रश्न
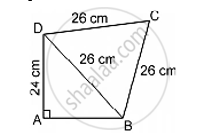
Find the area of the quadrilateral ABCD in which AD = 24 cm, ∠BAD 90° and ∠BCD is an equilateral triangle having each side equal to 26 cm. Also, find the perimeter of the quadrilateral.
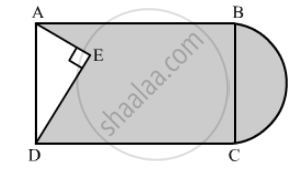
In the following figure, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside' the region. Find the area of the shaded region. [Use π =]`22/7` [CBSE 2014]
In the following figure, there are three semicircles, A, B and C having diameter 3 cm each, and another semicircle E having a circle D with diameter 4.5 cm are shown. Calculate:
(i) the area of the shaded region
(ii) the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.

In the following figure, the boundary of the shaded region consists of four semi-circular arcs, the smallest two being equal. If the diameter of the largest is 14 cm and of the smallest is 3.5 cm, find
the length of the boundary.
the area of the shaded region.

The circumference of a circle is 100 m. The side of a square inscribed in the circle is
The area of the incircle of an equilateral triangle of side 42 cm is
The area of incircle of an equilateral triangle is 154 cm2 . The perimeter of the triangle is
Two circles touch externally. The sum of their areas is 130π sq. cm and the distance between their centers is 14 cm. Find the radii of the circles.
Find the area of a circle of radius 30 cm (use π = 3.14).
The floor of the circular swimming pool whose radius is 7 m has to be cemented at the rate of ₹ 18 per m2. Find the total cost of cementing the floor
