Advertisements
Advertisements
प्रश्न
The floor of the circular swimming pool whose radius is 7 m has to be cemented at the rate of ₹ 18 per m2. Find the total cost of cementing the floor
उत्तर
Radius of the circular swimming pool r = 7 m
Area of the circular swimming pool A = πr2 sq.units
= `22/7 xx 7 xx 7 "m"^2`
= 154 m2
Cost of cementing a m2 floor = ₹ 18
Cost of cementing 154 m2 floor = ₹ 18 × 154
= ₹ 2,772
APPEARS IN
संबंधित प्रश्न
The area of rectangle is `192cm^2` and its perimeter is 56 cm. Find the dimensions of the rectangle.
Find the area of a parallelogram with base equal to 25 cm and the corresponding height measuring 16.8 cm.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the sector formed by the arc. (Use π = `22/7`)
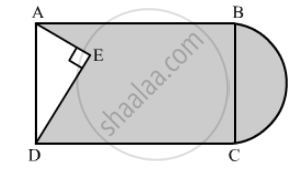
In the following figure, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside' the region. Find the area of the shaded region. [Use π =]`22/7` [CBSE 2014]
In the following figure, AB = 36 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all the three circles. Find the area of the shaded region.

A circular park has a path of uniform width around it. The difference between the outer and inner circumferences of the circular path is 132 m. Its width is
The area of the sector of a circle of radius 10.5 cm is 69.3 cm2. Find the central angle of the sector.
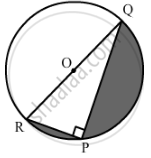
In the given figure, PQ = 24, PR = 7 cm and O is the centre of the circle. Find the area of the shaded region.
The diameters of two circles are 32 cm and 24 cm. Find the radius of the circle having its area equal to the sum of the areas of the two given circles.
The diameters of three wheels are in the ratio 2 : 4 : 8. If the sum of the circumferences of these circles be 132 cm, find the difference between the areas of the largest and the smallest of these wheels.
