Advertisements
Advertisements
प्रश्न
In the following figure, AB = 36 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all the three circles. Find the area of the shaded region.

उत्तर
We have given two semi-circles and one circle.
Area of the shaded region = area of semicircle with diameter AB − area of two semicircles with diameters AM and MB - area of circle ……..(1)
Let us calculate the area of the semi-circle with AB as a diameter.
`"Area of semi-circle with AB as a diameter "= pir^2/2`
`∴ "Area of semi-circle with AB as a diameter "=(pi(36/2)^2)/2`
`"∴Area of semi-circle with AB as a diameter"=(pixx18^2)/2`
Now we will find the area of the semi-circle with AM as a diameter.
`"∴Area of semi-circle with AM as a diameter"=(pi r^2)/2`
`"∴Area of semi-circle with AM as a diameter"=pi(18/2)^2`
`"∴Area of semi-circle with AM as a diameter"=(pixx9^2)/2`
with diameter with AM as a diameter.
Now we will find the area of the circle with centre C.
Area of circle=`pir^2`
We know that radius of the circle is one sixth of AB
Area of circle=`pixx6^2`
Now we will substitute all these values in equation (1).
`∴"Area of shaded region"=(pixx18^2)/2-(pixx9^2)/2-(pixx9^2)/2-36pi`
`∴"Area of shaded region"=pixx18^2/2-pixx9^2-36pi`
`"∴Area of shaded region"=(pixx18^2)/2-81 pi-36pi`
`"∴ Area of shaded region"=(pixx18^2)/22-117pi`
`"∴Area of shaded region"=(162-117)pi`
`∴"Area of shaded region"=45pi`
Therefore, area of shaded region is `45 pi cm^2`
APPEARS IN
संबंधित प्रश्न
Find the area of a parallelogram with base equal to 25 cm and the corresponding height measuring 16.8 cm.
A chord of a circle of radius 20 cm sub tends an angle of 900 at the centre . Find the area of the corresponding major segment of the circle
( Use \[\pi = 3 . 14\])
The ratio of the areas of a circle and an equilateral triangle whose diameter and a side are respectively equal, is
The area of a circular path of uniform width h surrounding a circular region of radius r is
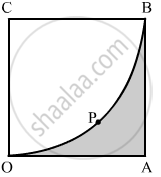
In the given figure, OABC is a square of side 7 cm. If COPB is a quadrant of a circle with centre C find the area of the shaded region.
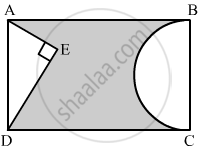
In the given figure, ABCD is a rectangle with AB = 80 cm and BC = 70 cm, ∠AED = 90° and DE = 42 cm. A semicircle is drawn, taking BC as diameter. Find the area of the shaded region.
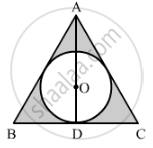
In the given figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region.
[Use `sqrt(3)= 1.73, pi = 3.14]`
The diameters of three circles are in the ratio 3: 5: 6. If the sum of the circumferences of these circles is 308 cm; find the difference between the areas of the largest and the smallest of these circles.
Find the area of the shaded portion in each of the following diagrams:
(i)

(ii)

Is the area of the largest circle that can be drawn inside a rectangle of length a cm and breadth b cm (a > b) is πb2 cm2? Why?
