Advertisements
Advertisements
प्रश्न
In the given figure, OABC is a square of side 7 cm. If COPB is a quadrant of a circle with centre C find the area of the shaded region.
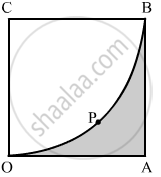
उत्तर
Area of shaded region = Area of square OABC − Area of quadrant COPB having radius OC
`= (Side)^2 - 1/4(pixx"r"^2)`
`=(7)^2 - 1/4[22/7xx7^2]`
= 49 - 38.5
= 10.5 cm2
Area of shaded region = Area of square OABC − Area of quadrant COPB having radius OC
APPEARS IN
संबंधित प्रश्न
From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1 cm are removed. (as shown in the following figure). Find the area of the remaining sheet. (Take `pi = 22/7`)

A circle is inscribed in an equilateral triangle ABC is side 12 cm, touching its sides (the following figure). Find the radius of the inscribed circle and the area of the shaded part.

In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the area of the cross-section.
If the circumference of two circles are in the ratio 2 : 3, what is the ratio of their areas?
If the difference between the circumference and radius of a circle is 37 cm, then using π = \[\frac{22}{7}\] the circumference (in cm) of the circle is
The minute hand of a clock is 8 cm long. Find the area swept by the minute hand between 8.30 a.m. and 9.05 a.m.
A bicycle wheel, diameter 56 cm, is making 45 revolutions in every 10 seconds. At what speed in kilometre per hour is the bicycle traveling?
Find the area of the circle, length of whose circumference is equal to the sum of the lengths of the circumferences with radii 15 cm and 13 cm.
The diameters of three wheels are in the ratio 2 : 4 : 8. If the sum of the circumferences of these circles be 132 cm, find the difference between the areas of the largest and the smallest of these wheels.
The sum of diameters of two circles is 112cm and the sum of their areas is 5236cm2. Find the radii of the two circles.
