Advertisements
Advertisements
प्रश्न
In the following figure, AB = 36 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all the three circles. Find the area of the shaded region.

उत्तर
We have given two semi-circles and one circle.
Area of the shaded region = area of semicircle with diameter AB − area of two semicircles with diameters AM and MB - area of circle ……..(1)
Let us calculate the area of the semi-circle with AB as a diameter.
`"Area of semi-circle with AB as a diameter "= pir^2/2`
`∴ "Area of semi-circle with AB as a diameter "=(pi(36/2)^2)/2`
`"∴Area of semi-circle with AB as a diameter"=(pixx18^2)/2`
Now we will find the area of the semi-circle with AM as a diameter.
`"∴Area of semi-circle with AM as a diameter"=(pi r^2)/2`
`"∴Area of semi-circle with AM as a diameter"=pi(18/2)^2`
`"∴Area of semi-circle with AM as a diameter"=(pixx9^2)/2`
with diameter with AM as a diameter.
Now we will find the area of the circle with centre C.
Area of circle=`pir^2`
We know that radius of the circle is one sixth of AB
Area of circle=`pixx6^2`
Now we will substitute all these values in equation (1).
`∴"Area of shaded region"=(pixx18^2)/2-(pixx9^2)/2-(pixx9^2)/2-36pi`
`∴"Area of shaded region"=pixx18^2/2-pixx9^2-36pi`
`"∴Area of shaded region"=(pixx18^2)/2-81 pi-36pi`
`"∴ Area of shaded region"=(pixx18^2)/22-117pi`
`"∴Area of shaded region"=(162-117)pi`
`∴"Area of shaded region"=45pi`
Therefore, area of shaded region is `45 pi cm^2`
APPEARS IN
संबंधित प्रश्न
The cost of fencing a square lawn at ₹ 14 per meter is ₹ 28000. Find the cost of mowing the lawn at ₹ 54 100 per `m^2`
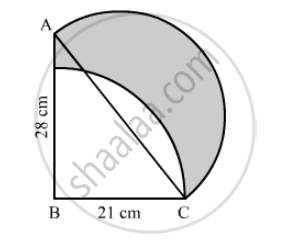
In the following figure, ABC is a right-angled triangle, ∠B = 90°, AB = 28 cm and BC = 21 cm. With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
The length of an arc of the sector of angle θ° of a circle with radius R is
A steel wire, when bent in the form of a square, encloses an area of 121 cm2. The same wire is bent in the form of a circle. Find area the circle.
Two circles touch each other externally. The sum of their areas is 58πcm2 and the distance between their centres us 10cm. Find the radii of the two circles.
A square is inscribed in a circle of radius 6 cm. Find the area of the square. Give your answer correct to two decimal places if `sqrt(2)` = 1.414.
Find the area of the dining table whose diameter is 105 cm
What is the diameter of a circle whose area is equal to the sum of the areas of two circles of radii 40cm and 9cm?
If the radius of a semi-circular protractor is 7cm, then its perimeter is ______.
