Advertisements
Advertisements
प्रश्न
In the following figure, ABC is a right-angled triangle, ∠B = 90°, AB = 28 cm and BC = 21 cm. With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
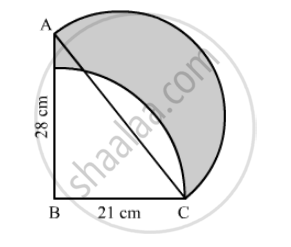
उत्तर
We have given two semi-circles and one circle.
Area of the shaded region = area of semicircle with diameter AC + area of right angled triangle ABC − area of sector
First we will find the hypotenuse of right angled triangle ABC.
`AC^2=AB^2+BC^2`
`∴ AC^2=28^2+21^2`
`∴ AC^2=784+441`
`∴ AC^2=1225`
`∴ AC=35`
`∴ "Area of the shaded region"=(pixx17.5xx17.5)/2+1/2xx28xx21-θ/360xxpixx21xx21`
`∴ "Area of the shaded region"=(pixx17.5xx17.5)/2+14xx21-1/4xxpixx21xx21`
Substituting `pi=22/7`we get,
`∴ "Area of shabed region"=(22/7xx17.5xx17.5)/2+14xx21-1/4xx22/7xx21xx21`
`∴ "Area of shabed region"=962.5/2+14xx21-1/2xx11xx3xx21`
`∴ "Area of shabed region"=481.25+294-346.5`
`∴ "Area of shabed region"=428-75`
Therefore, area of shaded region is `428.75 cm^2`
APPEARS IN
संबंधित प्रश्न
The adjacent sides of a parallelogram are 32 cm and 24 cm. If the distance between the longer sides is 17.4 cm, find the distance between the shorter sides.
The ratio of the areas of a circle and an equilateral triangle whose diameter and a side are respectively equal, is
If diameter of a circle is increased by 40%, then its area increase by
In the given figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region. [Use π= 3.14]

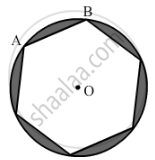
A round table cover has six equal designs as shown in the given figure. If the radius of the cover is 35 cm, then find the total area of the design.
The diameters of two circles are 32 cm and 24 cm. Find the radius of the circle having its area equal to the sum of the areas of the two given circles.
Two circles touch externally. The sum of their areas is 130π sq. cm and the distance between their centers is 14 cm. Find the radii of the circles.
In a grassland, a sheep is tethered by a rope of length 4.9 m. Find the maximum area that the sheep can graze
The radii of the two circles are 4 cm and 3 cm respectively. The diameter of the circle having an area equal to the sum of the areas of the two circles (in cm) is ____________.
A pendulum swings through an angle of 30∘ and describes an arc 8.8 cm in length. Find the length of the pendulum in cm.
