Advertisements
Advertisements
प्रश्न
In the following figure, ABC is a right-angled triangle, ∠B = 90°, AB = 28 cm and BC = 21 cm. With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
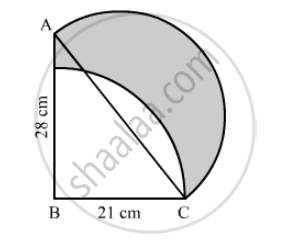
उत्तर
We have given two semi-circles and one circle.
Area of the shaded region = area of semicircle with diameter AC + area of right angled triangle ABC − area of sector
First we will find the hypotenuse of right angled triangle ABC.
`AC^2=AB^2+BC^2`
`∴ AC^2=28^2+21^2`
`∴ AC^2=784+441`
`∴ AC^2=1225`
`∴ AC=35`
`∴ "Area of the shaded region"=(pixx17.5xx17.5)/2+1/2xx28xx21-θ/360xxpixx21xx21`
`∴ "Area of the shaded region"=(pixx17.5xx17.5)/2+14xx21-1/4xxpixx21xx21`
Substituting `pi=22/7`we get,
`∴ "Area of shabed region"=(22/7xx17.5xx17.5)/2+14xx21-1/4xx22/7xx21xx21`
`∴ "Area of shabed region"=962.5/2+14xx21-1/2xx11xx3xx21`
`∴ "Area of shabed region"=481.25+294-346.5`
`∴ "Area of shabed region"=428-75`
Therefore, area of shaded region is `428.75 cm^2`
APPEARS IN
संबंधित प्रश्न
Find the length of the hypotenuse of an isosceles right-angled triangle whose area is `200^2` cm . Also, find its perimeter
Each of the equal sides of an isosceles triangle measure 2 cm more than its height, and the base of the triangle measure 12 cm. Find the area of the triangle.
A calf is tied with a rope of length 6 m at the corner of a square grassy lawn of side 20 m . If the length of the rope is increased by 5.5 m , find the increase in area of the grassy lawn in which the calf can graze .
In the following figure, AB and CD are two diameters of a circle perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
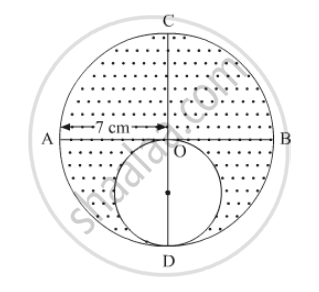
A circular park has a path of uniform width around it. The difference between the outer and inner circumferences of the circular path is 132 m. Its width is
A pendulum swings through an angle of 30° and describes an arc 8.8 cm in length. Find the length of the pendulum.
The radii of two circles are in the ratio 3: 8. If the difference between their areas is 2695π cm2, find the area of the smaller circle.
A steel wire, when bent in the form of a square, encloses an area of 121 cm2. The same wire is bent in the form of a circle. Find area the circle.
Find the area of the circle, length of whose circumference is equal to the sum of the lengths of the circumferences with radii 15 cm and 13 cm.
The area of the circle whose diameter is 21 cm is ____________.
