Advertisements
Advertisements
प्रश्न
A steel wire, when bent in the form of a square, encloses an area of 121 cm2. The same wire is bent in the form of a circle. Find area the circle.
उत्तर
Area of a square = ( Side )2
⇒ 121 = ( Side )2
⇒ Side of a square = 11 cm
Now,
The perimeter of a square = Perimeter of a circle
⇒ 4 x Side = Perimeter of a circle
⇒ 4 x 11 = Perimeter of a circle
⇒ Perimeter of a circle = 44 cm
⇒ 2πr = 44 ....( r is radius of a circle )
⇒ r = `44/[2π] = 44/[ 2 xx 22/7]` = 7 cm
∴ Area of a circle = πr2 = `22/7 xx 7 xx 7 = 154 "cm"^2`
APPEARS IN
संबंधित प्रश्न
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the sector formed by the arc. (Use π = `22/7`)
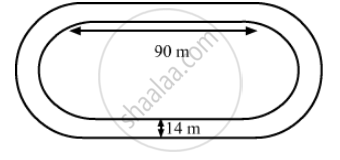
The inside perimeter of a running track (shown in the following figure) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If the track is everywhere 14 m wide. find the area of the track. Also find the length of the outer running track.
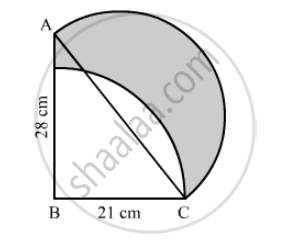
In the following figure, ABC is a right-angled triangle, ∠B = 90°, AB = 28 cm and BC = 21 cm. With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
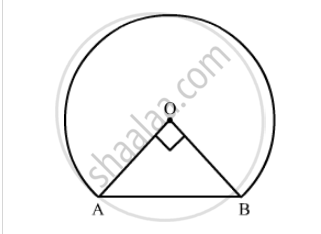
In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the perimeter of the cross-section
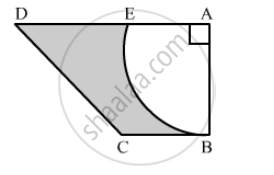
In the following figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region. [CBSE 2014]
The minute hand of a clock is 15 cm long. Calculate the area swept by it in 20 minutes.
A round table cover has six equal designs as shown in the given figure. If the radius of the cover is 35 cm, then find the total area of the design.
A chord of a circle of radius 14 cm a makes a right angle at the centre. Find the area of the sector.
Is the area of the circle inscribed in a square of side a cm, πa2 cm2? Give reasons for your answer.
A circular park is surrounded by a road 21 m wide. If the radius of the park is 105 m, find the area of the road.
