Advertisements
Advertisements
प्रश्न
The minute hand of a clock is 15 cm long. Calculate the area swept by it in 20 minutes.
उत्तर
Angle inscribed by the minute hand in 60 minutes = 360°
Angle inscribed by the miniute hand in 20 minutes`=360/60xx20=120°`
We have :
θ = 120 and r = 15 cm
∴ Required area swept by the miniute hand in 20 miniutes = Area of the sector with r = 15 cm and θ = 120°
`= (pi"r"^2theta)/360`
`=3.14xx15xx15xx120/360`
= 235.5 cm2
APPEARS IN
संबंधित प्रश्न
The cost of harvesting a square field at ₹ 900 per hectare is ₹ 8100. Find the cost of putting a fence around it at ₹ 18 per meter.
A chord of a circle of radius 20 cm sub tends an angle of 900 at the centre . Find the area of the corresponding major segment of the circle
( Use \[\pi = 3 . 14\])
Find the area of the circle in which a square of area 64 cm2 is inscribed. [Use π = 3.14]
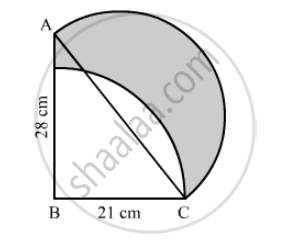
In the following figure, ABC is a right-angled triangle, ∠B = 90°, AB = 28 cm and BC = 21 cm. With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
The area of the largest triangle that can be inscribed in a semi-circle of radius r, is
In the following figure, the shaded area is

The radii of two circles are 8 cm and 6 cm. Find the radius of the circle having area equal to the sum of the areas of the two circles.
From a rectangular sheet of paper ABCD with AB = 40 cm and AD = 28 cm, a semicircular portion with BC as diameter is cut off. Find the area of the remaining paper.
The areas of two concentric circles are 1386 cm2 and 962.5 cm2. The width of the ring is
If a square in inscribed in a circle, find the ratio of the areas of the circle and the square.
