Advertisements
Advertisements
प्रश्न
A chord of a circle of radius 20 cm sub tends an angle of 900 at the centre . Find the area of the corresponding major segment of the circle
( Use \[\pi = 3 . 14\])
उत्तर
We know area of minor segment of the circle is \[A = \left\{ \frac{\pi\theta}{360} - \sin\frac{\theta}{2}\cos\frac{\theta}{2} \right\} r^2\]
\[\Rightarrow A = \left\{ \frac{\pi \times 90°}{360} - \sin\frac{90}{2}\cos\frac{90}{2} \right\} \left( 20 \right)^2 \]
\[ \Rightarrow A = \left( \frac{\pi}{4} - \frac{1}{2} \right)\left( 400 \right)\]
Area of the major segment = Area of the circle − area of the minor segment
\[= \pi \left( 20 \right)^2 - \left( 400 \right)\left[ \frac{\pi}{2} - \frac{1}{2} \right]\]
\[ = \left( 400 \right)\left[ \pi - \frac{\pi}{2} + \frac{1}{2} \right]\]
\[ = 1142 {cm}^2\]
APPEARS IN
संबंधित प्रश्न
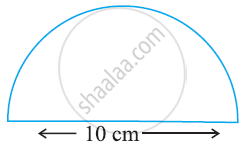
Find the perimeter of the adjoining figure, which is a semicircle including its diameter.
If diameter of a circle is increased by 40%, then its area increase by
In the following figure, the area of the segment PAQ is

What is the diameter of a circle whose area is equal to the sum of the areas of two circles of diameters 10 cm and 24 cm?
A square is inscribed in a circle. Find the ratio of the areas of the circle and the square.
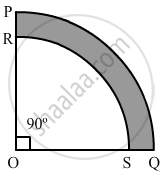
In the given figure, PQRS represents a flower bed. If OP = 21 m and OR = 14 m, find the area of the flower bed.
If a square in inscribed in a circle, find the ratio of the areas of the circle and the square.
Diameter of a circular garden is 9.8 m. Find its area.
A pendulum swings through an angle of 30∘ and describes an arc 8.8 cm in length. Find the length of the pendulum in cm.
Is the area of the circle inscribed in a square of side a cm, πa2 cm2? Give reasons for your answer.
